Die Kreiszahl π ist eine der faszinierendsten und wichtigsten Konstanten in der Mathematik. In diesem Lernpfad lernst du viele interessante Aspekte von π kennen und erhältst u. a. Antworten auf folgende Fragen:

• Wie ist π definiert?
• Ist π wie √2 irrational?
• In welchen Gleichungen taucht π auf?
• Wie kann man möglichst viele Stellen von π berechnen?
• Ist die Quadratur des Kreises mit Zirkel und Lineal möglich?

Wenn du in der Oberstufe bist, wirst du alle Inhalte des Lernpfads verstehen, wenn du Mittelstufenschüler bist, wirst du fast alle Lerninhalte (nicht den Reiter zur "Irrationalität und Transzendenz" und nicht den Abschnitt "Vorkommen in Formeln" im Reiter zu "Vorkommen von Pi") verstehen.

Wir fangen ganz einfach an:

π ist ganz schlicht und bescheiden nur das Verhältnis zwischen dem Umfang eines Kreises und dessen Durchmesser (siehe Bild). Also:

$π = \frac{U}{d}$

Vornehmer: Umfang und Durchmesser eines Kreises sind proportional zueinander, d. h.: Wenn man den Durchmesser verdoppelt, dann verdoppelt sich auch der Umfang. Der Proportionalitätsfaktor von Umfang und Durchmesser ist die Zahl π. (Leonhard Euler wählte deshalb den griechischen Buchstaben π für den Proportionalitätsfaktor, weil er der Anfangsstube von griech. peripheria = dt. Umfang ist. Aufgrund der großen Bedeutung von Euler wurde auch später diese Bezeichnungsweise verwendet.)

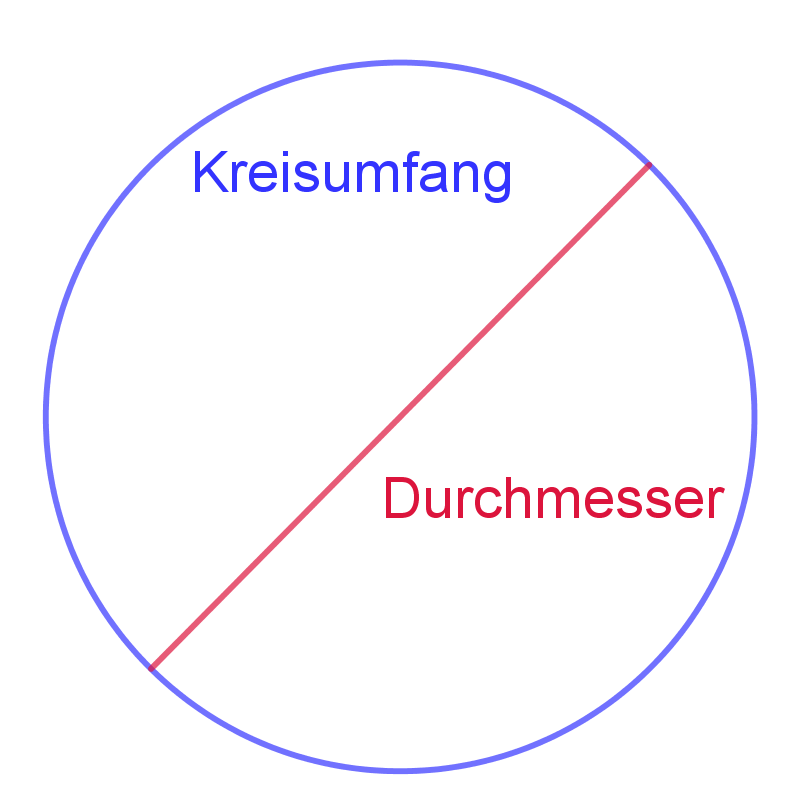
Miss nun Durchmesser und Umfang (am besten mit einem Faden) von Kreisformen aus dem Alltag (z. B. Teller, Tesafilmrolle) und berechne ihr Verhältnis. Du wirst, wenn du dir Mühe gibst und sorgfältig arbeitest, ungefähr 3,14 erhalten. Die Kreiszahl π ist wie √2 eine irrationale Zahl, sie hat also als Dezimalbruch geschrieben unendlich viele Stellen und keine Periode. 3,14 ist deshalb nur eine Näherung. Auch der Bruch 22/7 ist sehr gebräuchlich. Wie man π genauer berechnen kann, erfährst du auf den folgenden Reitern.

Man kann mit der Zahl π nicht nur den Kreisumfang berechnen, wenn der Durchmesser d oder der Radius r gegeben ist, nämlich mittels

U = π ⋅ d beziehungsweise U = 2⋅π⋅r,

sondern auch die Kreisfläche. Dazu zeichnest du einen ausreichend großen Kreis und schneidest ihn in 12 gleich große Teile (siehe Bild):

Die Teile legst du nun zu einem "Rechteck" (siehe Bild):

Das Rechteck hat ungefähr die Längen: π⋅r (die Hälfte des Umfangs) und r. Damit ergibt sich:

A = Länge mal Breite = π⋅r⋅r = π⋅r².

Die obige Herleitung wird umso genauer, je mehr Kreisteile du benutzt.

Wir fassen zusammen. Die Kreisfläche ist:

$A_{Kreis} = π⋅r^{2}$

Übrigens: Die Kreiszahl π wird auch Ludolphsche Zahl genannt, denn Ludolph van Ceulen berechnete im 16. Jahrhundert π auf 35 Dezimalstellen genau. Eine weitere Bezeichnung ist Archimedes-Konstante. Auf den nächsten Reitern wirst du verstehen, warum man diese Bezeichnung verwendet.

Aufgaben:

1.) Berechne Umfang und Flächeninhalt eines Kreises mit dem Durchmesser d = 7,20 m. (Lösung: U = 22,6 m, A = 40,7 m²)

2.) Berechne den Radius eines Kreises mit einem Flächeninhalt von 2,5 cm². (Lösung: r = 0,89 cm)

3.) Wie ändert sich der Flächeninhalt eines Kreises, wenn man seinen Durchmesser verdoppelt? (Lösung: Er vervierfacht sich.)

4.) Eine Raumfähre umkreist die Erde in einer Flughöhe von 275 km. Für eine Erdumkreisung benötigt die Raumfähre 1 1/2 Stunden. Berechne die Geschwindigkeit des Raumschiffs auf der Umlaufbahn um die Erde. Gehe dabei von 6 370 km für den Erdradius aus. (Lösung: v = 27 834,5 km/h)

Archimedes von Syrakus

Ungefähr 250 v. Chr. begann Archimedes, den Kreisumfang durch einbeschriebene und umbeschriebene regelmäßige Polygone zu approximieren. Wenn man die Anzahl der Polygonecken jeweils verdoppelt, so nähern sich die Polygonumfänge immer mehr dem Kreisumfang:

$\lim\limits_{n\to\infty}U_{n-Eck}=U_{Kreis}$

In den folgenden Rechnungen wird der Radius gleich 1 gesetzt, so dass $π=\frac{U}{2}$ gilt.

Die untere Skizze veranschaulicht, wie Archimdes beim einbeschriebenen Polygon vorgegangen ist: M ist der Mittelpunkt des Kreises und der Radius ist r=1.  Die Seite eines regelmäßigen Sechsecks ist $\overline{AC}=s_{n}$. Bei der Verdopplung zum Zwölfeck entstehen die Seiten $\overline{AB}$ und $\overline{BC}$ und werden mit $s_{2n}$ bezeichnet. In der nun folgenden Rechnung wird die Beziehung zwischen $s_{n}$ und $s_{2n}$ ermittelt.

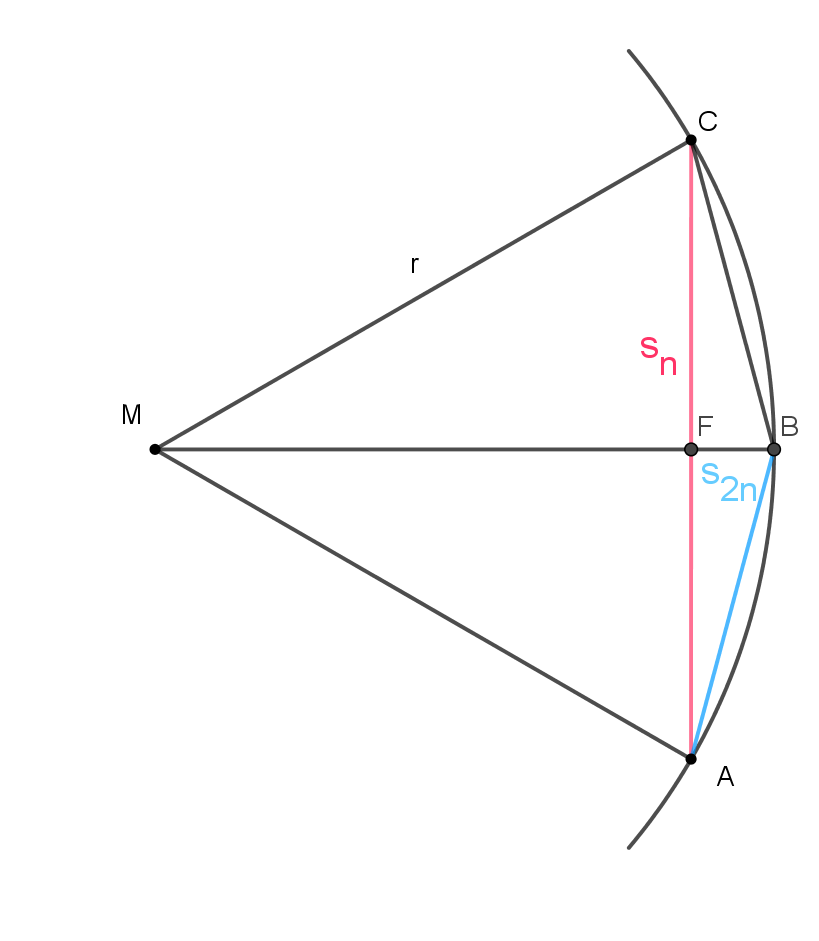
Da $\overline{MA}=r=1$ ist, folgt aus dem Satz des Pythagoras:

$\overline{AF}^{2}+\overline{MF}^{2} = 1 ⇔ \overline{MF}^{2} = 1 - \overline{AF}^{2}$

Für $\overline{AF} = \frac{s_{n}}{2}$ erhält man:

$\overline{MF} = \sqrt{1-(\frac{s_{n}}{2})^{2}}$ ⇔ $\overline{MF} = \frac{1}{2}\sqrt{4-s_{n}^{2}}  (1)$

Aus dem Satz des Pythagoras folgt auch: $\overline{AF}^{2} + \overline{FB}^{2} = \overline{AB}^{2} ⇔ \overline{FB}^{2} = \overline{AB}^{2} - \overline{AF}^{2}$

Mit $\overline{AB} = s_{2n}$ erhält man: $\overline{FB}=\sqrt{s_{2n}^{2}-(\frac{s_{n}}{2})^{2}} ⇔ \overline{FB} = \frac{1}{2}\sqrt{4s_{2n}^{2} - s_{n}^{2}}  (2)$

Es gilt $\overline{MF} + \overline{FB} = 1$ und mit den Formeln (1) und (2) folgt:

$\frac{1}{2}\sqrt{4 - s_{n}^{2}} + \frac{1}{2}\sqrt{4s_{2n}^{2} - s_{n}^{2}} = 1 ⇔ 1 - \frac{1}{2}\sqrt{4 - s_{n}^{2}} = \frac{1}{2}\sqrt{4s_{2n}^{2} - s_{n}^{2}}$

Jetzt werden beide Seiten quadriert:

$1 - 2 ⋅\frac{1}{2}\sqrt{4 - s_{n}^{2}} + \frac{1}{4}(4-s_{n}^{2}) = \frac{1}{4}(4s_{2n}^{2} - s_{n}^{2})$

⇔ $1-\sqrt{4 - s_{n}^{2}} + 1 - \frac{s_{n}^{2}}{4} = s_{2n}^{2} - \frac{s_{n}^{2}}{4}$

⇔ $s_{2n}^{2} = 2 - \sqrt{4 - s_{n}^{2}} ⇔ \underline{s_{2n} = \sqrt{2 - \sqrt{4 - s_{n}^{2}}}}$

Für den Umfang multipliziert man das $s_{2n}$ mit 2n: $\underline{u_{2n} = 2n ⋅ s_{2n}}$

Im nächsten Reiter führen wir ähnliche Rechnungen für die Approximation durch umbeschriebene Polygone durch.

Nun entwickeln wir eine Formel für den Umfang mittels umbeschriebener Polygone:

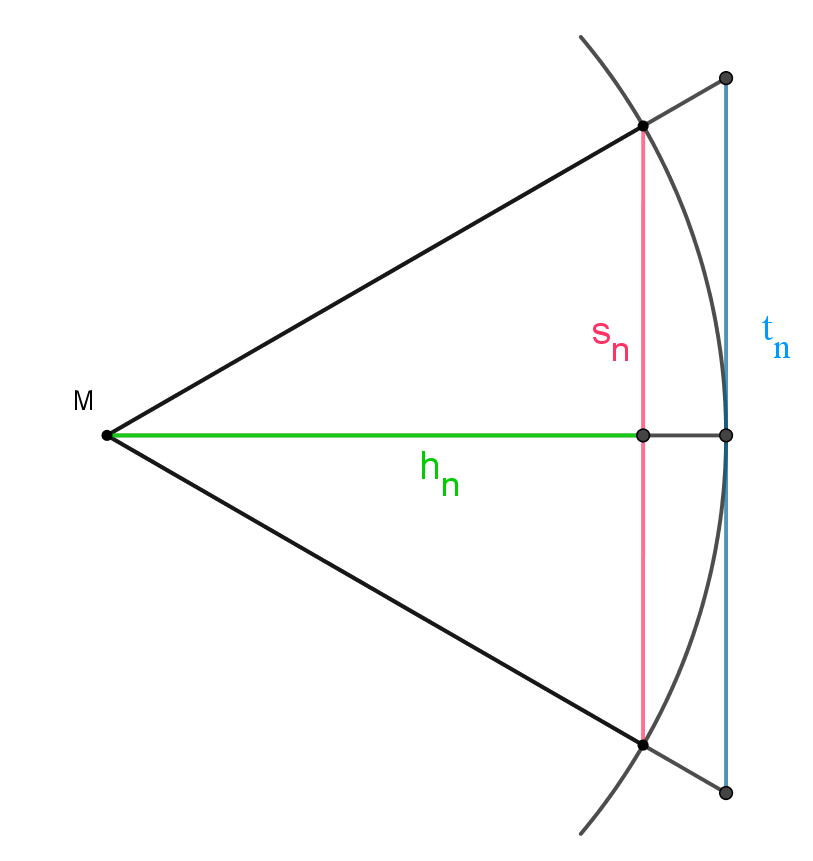
In der oberen Skizze ist $s_{n}$ wie im vorherigen Reiter eine Seite des einbeschriebenen n-Ecks. Hinzu kommt jetzt die Seite des umbeschriebenen n-Ecks namens $t_{n}$. Der Radius ist weiterhin 1.

Aus dem Strahlensatz folgt: $\frac{t_{n}}{s_{n}} = \frac{1}{h_{n}} ⇔ t_{n} = \frac{s_{n}}{h_{n}} (1) $

Für die grüne Seite $h_{n}$ gilt nach dem Satz des Pythagoras: $h_{n}^{2} = 1 - (\frac{s_{n}}{2})^2 ⇔ h_{n}=\sqrt{\frac{4 - s_{n}^{2}}{4}} ⇔ h_{n} = \frac{1}{2}\sqrt{4 - s_{n}^{2}}  (2) $

Nun setzen wir (2) in (1) ein und erhalten damit für $t_{n}$: $\underline{t_{n} = \frac{2⋅s_{n}}{\sqrt{4 - s_{n}^{2}}}}$

Für den Umfang des umbeschriebenen n-Ecks gilt entsprechend $\underline{U_{n} = n ⋅ t_{n} = n ⋅ \frac{2⋅s_{n}}{\sqrt{4 - s_{n}^{2}}}}$ 

Im folgendem Reiter werden wir schließlich die hergeleiteten Formeln in Excel nutzen, um die Zahl pi zu approximieren.

Unter Verwendung der Formeln der beiden vorherigen Reiter ergibt sich folgende Excel-Tabelle, die π auf sechs Dezimalstellen genau berechnet, wobei mit dem 6-Eck gestartet wurde:

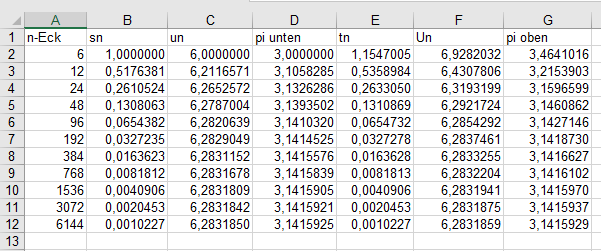
Wir haben gesehen, dass die Rechnungen einfach sind, aber dafür muss man Wurzelziehen, was in der Antike zu Archimedes Zeiten noch mühsam war. Die beschriebene Methode war bis ins 17. Jahrhundert trotz des sehr mühsamen Wurzelziehens die gebräuchlichste.

Des Weiteren erkannt man aus der Excel-Tabelle, dass der Wert für π nur sehr langsam konvergiert, bei jedem Schritt wird nur eine kleine Verbesserung erzielt. Das Verfahren ist also nicht anwendbar, wenn man mehrere Millionen Stellen berechnen will. Trotzdem ist es wegen seiner Einfachheit (Nur Mathematik-Wissen der Mittelstufe ist notwendig.) faszinierend.

Während schon die in den vorherigen Reitern beschriebene Approximation faszinierend ist, wird dich die jetzige Vorgehensweise zur Berechnung der Zahl π sehr überraschen:  

Mit Methoden der Wahrscheinlichkeitsrechnung werden wir im Folgenden den Wert von π approximieren. Da auch im Spielcasino von Monte-Carlo die Wahrscheinlichkeitsrechnung eine große Rolle spielt, nennt man diese Vorgehensweise die Monte-Carlo-Methode:

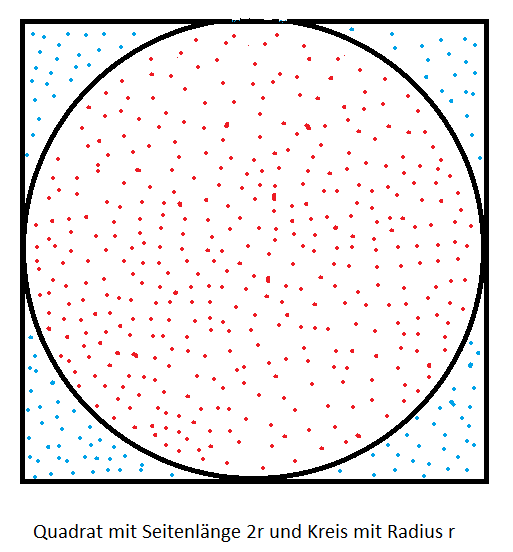
Man stelle sich zunächst einen Kreis mit Radius r in einem Quadrat mit Seitenlänge 2r vor (siehe Bild). Anschließend lässt man z. B. den Computer zufällig Punkte in dem Quadrat erzeugen. Man kann sich das so vorstellen, als würde man sehr oft einen Stift auf ein Blatt Papier fallen lassen. Nun zählt man, wie viele Punkte auf den Kreis (im Bild rot markiert) und wie viele auf das gesamte Quadrat (im Bild rot und blau markiert) fallen.

Der Kreis mit dem Radius r hat den Flächeninhalt $A_{Kreis} = π⋅r^{2}$ und das Quadrat hat den Flächeninhalt $A_{Quadrat} = (2r)^{2} = 4r^{2}$.

Das Verhältnis der Punkte im Kreis zu den Punkten im Quadrat entspricht nach dem Gesetz der großen Zahlen (siehe Gesetz der großen Zahlen) ungefähr dem Verhältnis der Flächen:

$\frac{A_{Kreis}}{A_{Quadrat}} ≈ \frac{Punkte\:im\:Kreis}{Punkte\:im\:Quadrat} ⇔ \frac{πr^{2}}{4r^{2}} ≈ \frac{Punkte\:im\:Kreis}{Punkte\:im\:Quadrat} ⇔$

$\frac{π}{4} ≈ \frac{Punkte\:im\:Kreis}{Punkte\:im\:Quadrat} ⇔ π ≈ 4 ⋅ \frac{Punkte\:im\:Kreis}{Punkte\:im\:Quadrat}$

Mit der folgenden Excel-Datei wird auf die oben beschriebene Weise der Wert von π approximiert:

Erste historische Schätzungen:

Das berühmteste Beispiel ist aus der Bibel: König Salomo gab dem Kupferschmied Hiram von Tyros den Auftrag, für den Jerusalemer Tempel ein kreisförmiges Wasserbecken (im Bibelzitat Meer genannt) herzustellen. Im ersten Buch der Könige - Kapitel 7 - Vers 23 heißt es: "Dann machte er das Meer. Es wurde aus Bronze gegossen und maß 10 Ellen von einem Rand zum anderen; es war völlig rund und 5 Ellen hoch. Eine Schnur von 30 Ellen konnte es rings umspannen." Eine Elle ist ungefähr 45 cm lang. Wenn man nun π berechnet, so ergibt sich immerhin $π = \frac{U}{d} ≈ \frac{30 Ellen}{10 Ellen} = 3$.

Das älteste bekannte Rechenbuch der Welt (Papyrus Rhind, 16. Jahrhundert vor Christus) verwendet als Näherung $(\frac{16}{9})^2 ≈ 3,1605$.

Die Babylonier nutzten den Wert $3 + \frac{1}{8} = 3,125$.

In Indien nutzte man die Näherungen $\sqrt{10} ≈ 3,1623$ oder später genauer $\frac{62832}{20000} = 3,1416$.

Der große Durchbruch gelang Archimedes mit der in den vorherigen Reitern beschriebenen Approximationsmethode. Sie erlaubte immer genauere Annäherungen. 

Für den Alltag reicht 3,14 oder der Bruch $\frac{22}{7}$. Der Näherungsrekord liegt bei 31,4 Billionen Nachkommastellen.

Vorkommen in Formeln:

Viel spannender ist das Vorkommen von π in Formeln. Da es sehr viele Formeln sind, folgt eine kleine Auswahl:

Eine sehr faszinierende Gleichung wurde von Euler 1748 aufgestellt und stellt eine einfache Verbindung zwischen der Kreiszahl π, der Eulerschen Zahl e und der Quadratwurzel aus -1, also i, her:

$e^{iπ} = -1 ⇔ e^{iπ} + 1 = 0$.

Diese Gleichung wird auch Eulersche Identität genannt und wird im nächsten Reiter zum Beweis der Transzendenz von π (d. h. π ist nicht Lösung einer polynomialen Gleichung mit ganzen oder rationalen Koeffizienten) genutzt. Sie gehört zu den 10 beeindruckendsten Formeln der Mathematik.

Die Kreiszahl kommt auch in vielen unendlichen Reihen vor:

Viele Mathematiker vor allem aus Basel (deshalb auch das Basler Problem genannt) fragten sich seit dem 17. Jahrhundert, wie groß die Summe aller reziproker Quadratzahlen ist. Es war wieder Euler, der 1735 die genial einfache Lösung fand:

$\frac{π^{2}}{6} = \frac{1}{1^{2}} + \frac{1}{2^{2}} + \frac{1}{3^{2}} +  ...$

Es gilt auch z. B. für die vierte Potenz:

$\frac{π^{4}}{90} = \frac{1}{1^{4}} + \frac{1}{2^{4}} + \frac{1}{3^{4}} +  ...$

Was erhalten wir, wenn wir nur die Summe der reziproken ungeraden Quadratzahlen betrachten? Auch dafür gibt es eine Lösung mit π:

$\frac{π^{2}}{8} = \frac{1}{1^{2}} + \frac{1}{3^{2}} + \frac{1}{5^{2}} +  ...$

Eine weitere sehr bekannte Reihe mit π ist die sogenannte Leibniz-Reihe, die Gottfried Wilhelm Leibniz 1682 veröffentlichte:

$\frac{π}{4} = \frac{1}{1} - \frac{1}{3} + \frac{1}{5} -  ...$

Gibt es statt einer unendlichen Summe auch ein unendliches Produkt mit π? Auch das gibt es. 1655 entwickelte der Engländer John Wallis eine solche Formel:

$\frac{π}{2} = \frac{2}{1} ⋅ \frac{2}{3} ⋅ \frac{4}{3} ⋅ \frac{4}{5} ⋅ \frac{6}{5} ⋅ \frac{6}{7} ⋅ \frac{8}{7} ⋅ \frac{8}{9} ⋅  ...$

Wir haben oben gezeigt, dass π keine rationale Zahl ist. Aber es kommt noch schlimmer: Während $\sqrt{2}$ auch irrational ist, ist sie wenigstens algebraisch, d.h. sie ist Lösung einer polynomialen Gleichung mit ganzzahligen oder rationalen Koeffizienten, in diesem Fall ist es die Gleichung $x^{2} - 2 = 0$. Eine nichtalgebraische Zahl wird als transzendent bezeichnet. 1882 konnte Ferdinand von Lindemann zeigen, dass π transzendent ist. Wie hat er das gemacht?

Die Vorarbeit leistete 1873 Charles Hermite. Er zeigte, dass die Eulersche Zahl e transzendent ist. Ferdinand von Lindemann zeigte, dass die Eulersche Zahl e, wenn sie mit einer algebraischen Zahl ungleich Null potenziert wird, transzendent ist (Anders formuliert: Ist α≠0 eine algebraische Zahl, so ist $e^{α}$ transzendent). Wir brauchen auch noch die Eulersche Formel: $e^{iπ} = -1$. Jetzt haben wir alle Zutaten für den Widerspruchsbeweis:

Wir nehmen an, dass π algebraisch sei. Die imaginäre Einheit i ist algebraisch, denn sie ist Lösung der Gleichung $x^{2} + 1 = 0$. Man kann zeigen, dass auch das Produkt zweier algebraischer Zahlen wieder algebraisch ist. Also ist iπ eine algebraische Zahl. Weiter folgen wir nach Lindemann, dass $e^{iπ}$ transzendent ist, denn die Eulersche Zahl e wird mit einer algebraischen Zahl ungleich Null potenziert. Also ist -1 transzendent. Die Zahl -1 ist aber Lösung der Gleichung x+1 = 0 und somit algebraisch. Nun haben wir den Widerspruch. Die Annahme ist falsch. Also ist π transzendent.

Wenn du dich fragst, ob es mehr algebraische oder mehr transzendente Zahlen gibt, dann lautet die überraschende Antwort, dass es wesentlich mehr transzendente als algebraische Zahlen gibt, so gesehen ist π nichts Außergewöhnliches.

Noch erstaunlicher ist die Konsequenz aus der Transzendenz von π: Die Griechen der Antike hatten drei Lieblingsprobleme, die sie nur in endlich vielen Schritten mit Zirkel und Lineal ohne Maßeinteilungen lösen wollten:

• die Quadratur des Kreises (aus einem gegebenen Kreis ein Quadrat mit demselben Flächeninhalt zu konstruieren)
• die Dreiteilung des Winkels (einen gegebenen Winkel in drei gleich große Winkel zu unterteilen)
• die Würfelverdopplung (das Volumen eines gegebenen Würfels zu verdoppeln)

Leider stellte sich erst im 19. Jahrhundert mithilfe algebraischer Methoden heraus, dass alle drei Probleme nur mit Zirkel und Lineal nicht lösbar sind.

Für die Quadratur des Kreises können wir die Unlösbarkeit jetzt begründen: Die Quadratur des Kreises, also die Konstruktion eines Quadrats mit demselben Flächeninhalt wie der des Kreises, ist äquivalent zur Konstruktion einer Geraden der Länge π, wobei man von einer Geraden der Länge 1 ausgeht. Man kann zeigen, dass jede Zahl, die sich auf diese Weise konstruieren lässt, algebraisch sein muss. Da π, wie wir oben gesehen haben, nicht algebraisch ist, ist die Konstruktion nicht möglich.

Trotzdem versuchen viele Hobbymathematiker, die Quadratur des Kreises zu lösen. Du darfst ab jetzt wohlwollend über diese Versuche lächeln.

Dein Wissen über die Kreiszahl π kannst du noch durch folgende Themen vertiefen, die in diesem Lernpfad nicht behandelt werden und hier nur kurz benannt werden:

Warum nicht den umgekehrten Weg gehen? Die Cusanus-Approximation:

Cusanus schachtelte nicht einen vorgegebenen Kreis durch ein- und umbeschriebene regelmäßige Vielecke
wie Archimedes ein, sondern er schachtelte ein vorgegebenes regelmäßiges Vieleck fester Umfangslänge durch ein- und umbeschriebene Kreise ein.

Goethes Faust in π? Oder: Ist π normal?

Eine Zahl ist genau dann normal, wenn man jede beliebige Kombination aus Ziffern in der Abfolge ihrer Nachkommastellen finden kann. Das hätte folgende faszinierende Konsequenz: Man könnte z. B. Goethes Faust in eine Zahlenfolge kodieren und würde genau diese Zahlenfolge in den Nachkommastellen einer normalen Zahl finden. Man würde sogar alle Bücher, die jemals geschrieben worden sind und in Zukunft geschrieben werden und nie geschrieben worden sind, in einer normalen Zahl finden. (Das würdest du sicherlich nicht als normal bezeichnen, aber wir müssen uns hier nach der Definition von normal in der Mathematik richten.) Es ist noch nicht bewiesen, ob π normal ist. Empirische Untersuchungen weisen allerdings auf die Normalität von π hin. 

Ist die Quadratur des Kreises näherungsweise möglich?

Im Lernpfad haben wir gelernt, dass aufgrund der Transzendenz von π die Quadratur des Kreises nur mit Zirkel und Lineal ohne weitere Hilfsmittel bzw. die Konstruktion einer Strecke mit der Länge von π nur mit Zirkel und Lineal nicht möglich ist. Es gibt jedoch sowohl viele Zirkel-und-Lineal-Konstruktionen, die sehr gute Näherungen liefern, als auch Konstruktionen, die mit einem weiteren Hilfsmittel zusätzlich zu Zirkel und Lineal eine genaue Konstruktion ermöglichen.

Wann ist Pi-Day?

Jedes Jahr wird der Pi-Day gefeiert. Wann er ist und welche Aktivitäten dann staffinden, dazu findest du viele Informationen im Internet.

Kann man π noch anders als durch einen Bruch oder einen Dezimalbruch darstellen?

Es gibt noch eine weitere sehr interessante Darstellung der Zahl π, nämlich die sogenannte Kettenbruchdarstellung. Sie ist zwar kompliziert, aber sehr lehrreich, um noch mehr über π zu erfahren.

Pi mit Nadeln?

Es gibt außer der hier behandelten Monte-Carlo-Methode noch ein weiteres Verfahren, um π mit stochastischen Mitteln zu approximieren: Das Buffonsche Nadelproblem.