Die Irrationalität von Wurzel 2
- Einführung
- Lösungsversuche
- Beweisidee
- Beweis des Euklid
- Biografien
- Aufgaben und Quize
- Lösungen
- Ausblick
Einführung
Wir schreiben das Jahr 470 vor Christus. Nein, liebe Schüler, es geht nicht so weiter wie bei Asterix und Obelix. Rom war damals nur ein armseliges Dorf, aber Pythagoras, ein Euch allen bekannter Grieche, unterrichtete seine Schüler in seiner Schule in Kroton im damals griechisch besiedelten Unteritalien. Es wurden gerade Flächen und Längen gepaukt. Hippasos von Metapont, sein begabtester Schüler, stellte Pythagoras eine wichtige Frage, indem er sich die folgende Figur, die er am Strand in den Sand gezeichnet hatte, genau anschaute:
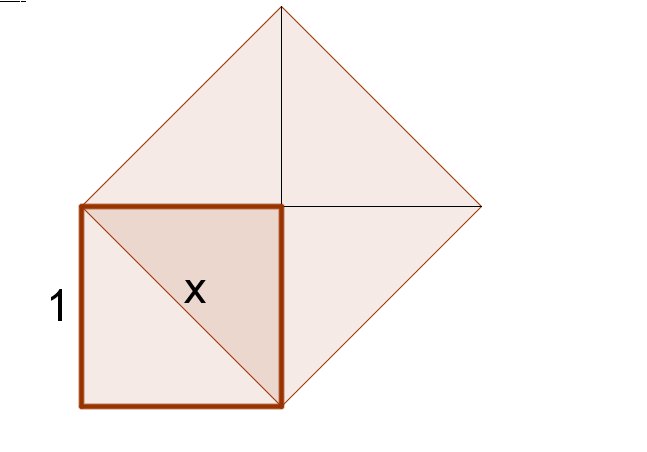
"Pythagoras, das kleine Quadrat hat die Länge 1 Fuß und die Fläche 1 Fuß ins Quadrat. Das große schräg liegende Quadrat hat die Fläche 2 Fuß ins Quadrat, aber ich kann die Länge nicht genau bestimmen." "Das kann nicht sein, das ist unmöglich!", lautete die entsetzte Antwort von Pythagoras, "versuche es doch mal mit 1,4 Fuß!".
1,4²=1,96. Das ist noch ziemlich weit von 2 entfernt. Probieren wir es mit 1,5: 1,5²=2,25, auch ziemlich weit weg. Erweitern wir auf die hunderstel Stelle, also auf z.B. 1,41: 1,41²= 1,9881. Schon besser. Vielleicht klappt es ja mit 1,42? 1,42²= 2,0164. Das sieht schon wesentlich besser aus, aber knapp daneben ist auch vorbei.
Wenn Ihr noch mal live den vielleichst aufregendsten Moment in der Geschichte der Mathematik erleben wollt, dann schaut Euch den Film von br-alpha an:
Auf dem nächsten Reiter überlegen wir, wie wir das Problem lösen können. Finden wir doch noch eine Zahl, deren Quadrat genau 2 ergibt?
Lösungsversuche
Wir überlegen: Wenn das Quadrat die Fläche 2 hat, dann, so haben wir gelernt, hat das Quadrat die Länge √2, denn √2*√2=2. Super, das Problem scheint gelöst zu sein. Jetzt geben wir nur noch √2 in den Taschenrechner ein, er spuckt als Lösung aus: 1,4142135623730950488016887242097. Hätten Pythagoras und Hippasos doch nur einen Taschenrechner gehabt.
Machen wir sicherheitshalber noch die Probe: Wir quadrieren und erhalten nicht 2. Wir sind zwar ganz ganz nah, aber es ist nicht exakt 2. Wenn wir uns noch so anstrengen, 100 Stellen, 1000 Stellen hinter dem Komma, wir erhalten nie 2. Erst viel später erkannte man, dass es unmöglich ist. Die √2, immerhin so etwas Gewöhnliches wie die Diagonalenlänge im Einheitsquadrat oder die Länge eines Quadrats mit der Fläche 2, ist eine so genannte irrationale Zahl, das heißt, sie hat unendlich viele Stellen ohne Periode. Ja, man kann noch nicht einmal einen Bruch finden, der √2 ergeben würde.
Beweisidee
Die Beweisidee und der eigentliche Beweis auf dem nächsten Reiter sind genial, aber schwierig. Habt mit Euch selbst Geduld! Beim ersten Durchlesen werdet Ihr vielleicht noch nicht alles verstehen. Lest deshalb die Beweisidee und den Beweis auf dem nächsten Reiter immer wieder durch und macht oft beim Lesen eine Pause!
Die Beweisführung erfolgt indirekt nach der Methode des Widerspruchsbeweises, das heißt, es wird gezeigt, dass die Annahme, die Wurzel aus 2 sei eine rationale Zahl, zu einem Widerspruch führt.
Ein einfaches Beispiel soll Euch die Widerspruchsbeweistechnik zeigen:
|
Um zu zeigen, dass nicht alle Menschen Deutsche sind, wird zunächst das genaue Gegenteil angenommen, nämlich dass alle Menschen Deutsche sind. Aus dieser Annahme folgt zum Beispiel, dass Churchill ein Deutscher war. Es ist aber bekannt, dass Churchill kein Deutscher war (sondern Engländer). Dass Churchill aber zugleich sowohl ein Deutscher als auch kein Deutscher war, ist ein Widerspruch. Damit wurde die Aussage, dass alle Menschen Deutsche sind, auf einen Widerspruch zurückgeführt (reductio ad absurdum) und so gezeigt, dass nicht alle Menschen Deutsche sind. |
Nun seid Ihr vorbereitet für den nächsten Reiter:
Beweis des Euklid
Es folgt nun der so genannte Beweis des Euklid, weil Euklid ihn in seinen "Elementen" aufschrieb, allerdings in heutiger Sprache: (Mehr über Euklid erfahrt Ihr auf dem Reiter Biografien)
| Beweis des Euklid: |
Kommentar: |
|
(1) Annahme: √2=p/q, wobei p und q teilerfremde Zahlen sind. (2) 2 = (p/q)² <=> 2= p²/q² (3) 2*q²=p² (4) p² ist teilbar durch 2. (5) p ist teilbar durch 2. Also p = 2*r, wobei r eine ganze Zahl ist. (6) 2*q²=(2*r)²=4*r² <=> q²=2*r² (7) q² ist teilbar durch 2. (8) q ist teilbar durch 2. (8) ist mit (5) ein Widerspruch zu (1). |
Wir nehmen an, dass es eine Darstellung von √2 als Bruch gibt. Also kann man im Schritt (1) √2 auch als gekürzten Bruch p/q schreiben. Mit den Schritten (2) - (5) zeigt man, dass p gerade ist. Mit den Schritten (6) - (8) zeigt man, dass auch q gerade ist. (5) und (8) ergeben einen Widerspruch zu (1), denn dort wird angenommen, dass p/q ein gekürzter Bruch ist. Dieser Widerspruch zeigt: Es kann keine Darstellung von √2 als Bruch geben; √2 ist eine irrationale Zahl. |
In einem Video von echteinfach.tv und in einem Rap von Dorfuchs kannst du den Beweis nochmal anschauen und sogar nachsingen. Klicke dazu auf den folgenden Link: Video und Rap zum Beweis
Biografien
| Euklid | Hippasos | Pythagoras |
 |
 |
 |
|
|
Zur Biografie | Zur Biografie |
Aufgaben
Kreuzworträtsel zu irrationalen Zahlen
Kreuzworträtsel
| rationale | Die √9 ist eine ... Zahl. | |
| Pythagoras | Berühmter griechischer Mathematiker | der im 5. Jahrhundert vor Christus lebte. |
| Widerspruchsbeweis | Der Beweis des Euklid ist ein ... . | |
Euklid |
Der Beweis zur Irrationalität von √2 stammt von ... . | |
| Bruch | Jede rationale Zahl lässt sich als ... darstellen. | |
| irrationale | Die √5 ist eine ... Zahl. | |
| reellen | Rationale Zahlen und irrationale Zahlen bilden die Obermenge der ... Zahlen. | |
| Hippasos | Schüler von Pythagoras | der als erster die Irrationalität von √2 entdeckte. |
.. basiert auf dem Quiz-Skript Framework
Lösungen
Lösungen zu den ersten beiden Aufgaben des vorherigen Reiters:
|
Aufgabe 1.) (1) Wir nehmen an, dass √9=p/q, wobei p und q teilerfremd sind. (2) 9=p²/q² (3) 9q²=p² => (4) p² ist durch 9 teilbar (5) p ist durch 3 teilbar; sei p=3r (6) 9q²=9r² => (7) q²=r² (8) q=r=p/3 (8) eingesetzt in (1) ergibt: √9=3
|
Aufgabe 2.) (1) Wir nehmen an, dass √p=a/b, wobei a und b teilerfremd sind mit p als Primzahl (2) p=a²/b² (3) pb²=a² => (4) a² ist durch p teilbar (5) a ist durch p teilbar; sei a=pr (6) pb²=p²r² => (7) b²=pr² (8) b² ist durch p teilbar => (9) b ist durch p teilbar (9) und (5) sind ein Widerspruch zu (1) |
Ausblick
Die Menge der bisher im Unterricht behandelten rationalen Zahlen und die Menge der irrationalen Zahlen fasst man zur Obermenge der reellen Zahlen zusammen. Ihr werdet also in Zukunft mit reellen Zahlen rechnen müssen.
Damals brach für Pythagoras eine Welt zusammen, denn er glaubte, mit natürlichen Zahlen und mit Brüchen oder Verhältnissen von natürlichen Zahlen könne man alles, was es auf der Welt gibt, darstellen. Dadurch, dass es nicht so ist, verlor die Mathematik zunächst an Schönheit und an Einfachheit. Aber die Eleganz und Genialität des vorgestellten Widerspruchsbeweises sollte allen ein Trost sein.
Es ist überliefert, dass Pythagoras ziemlich sauer auf Hippasos war: Eine Legende erzählt, dass Hippasos aus dem Bund der Schüler von Pythagoras ausgeschlossen wurde und er als Strafe der Götter bei einem Schiffsuntergang im Meer ertrunken sei. Wenn ihr mehr über Hippasos und Pythagoras erfahren möchtest, dann klickt auf den Reiter Biografien.
