Liebe Schülerinnen und Schüler,

es klingt fast wie Zauberei: In diesem Lernpfad lernst du, wie man aus einem Rechteck nur mit dem Geodreieck , aber ohne den Millimetermaßstab zu benutzen, und einem Zirkel ein flächeninhaltsgleiches Quadrat konstruieren kann. Lediglich bei der Überprüfung, ob du richtig konstruiert hast, darfst du den Maßstab benutzen. Vornehm spricht man hier von der Quadratur des Rechtecks.

Auch die Frage, ob sogar die Quadratur des Dreiecks möglich ist, kann mit ja beantwortet werden. Ein Dreieck lässt sich nämlich leicht in ein flächeninhaltsgleiches Rechteck umwandeln. Anschließend führt man die Quadratur des Rechtecks durch. Man kann noch einen Schritt weitergehen: Auch die Quadratur des Polygons ist möglich, indem das Polygon in Dreiecke zerlegt wird, anschließend erfolgt die Umwandlung in ein flächeninhaltsgleiches Rechteck und schließlich führt man wieder die Quadratur des Rechtecks durch.

Bei so vielen guten Nachrichten wünscht man sich auch, dass die Quadratur des Kreises möglich ist. Hier ist das Ergebnis enttäuschend: Die Quadratur des Kreises nur mit Zirkel und Lineal ist leider nicht möglich. Näheres dazu erfährst du im Lernpfad über die Kreiszahl Pi.

Es gibt viele Methoden für die Quadratur des Rechtecks. In diesem Lernpfad lernst du die beiden einfachsten Methoden, nämlich die Quadratur mittels Höhensatz des Euklid (Porträt von Euklid siehe oben) und die Quadratur mittels Kathetensatz des Euklid, kennen. Der Höhensatz des Euklid und der Kathetensatz des Euklid bilden zusammen mit dem Satz des Pythagoras (Porträt von Pythagoras siehe unten) die sogenannte Satzgruppe des Pythagoras. Im nächsten Reiter wird der Satz des Pythagoras vorgestellt und bewiesen. Er dient als Grundlage für den im nächsten Reiter folgenden Höhensatz und den weiter folgenden Kathetensatz. Hier werden dir die Quadraturen Schritt für Schritt erklärt. Im Reiter Übungen findest du Aufgaben zum Üben der Quadraturen.

Alle drei Sätze der Satzgruppe des Pythagoras und damit auch Quadraturen wurden ca. 325 v. Chr. von Euklid in seiner Abhandlung, den Elementen, behandelt. Man kann davon ausgehen, dass Quadraturen schon vorher durchgeführt wurden.

Vorwissen

Um die Quadratur gut zu verstehen, solltest du Folgendes wissen:

• Begriffe beim rechtwinkligen Dreieck wie Katheten und Hypotenuse
• Konstuktion und Bedeutung des Thaleskreis
• Winkelsumme im Dreieck
• Gleichungen umstellen
• Wurzelziehen
• Binomische Formeln

Im unteren Bild siehst du ein rechtwinkliges Dreieck ABC mit den Katheten a und b und der Hypotenuse c. Über die Seiten sind die Quadrate $\mathrm{a^{2}}$, $\mathrm{b^{2}}$ und $\mathrm{c^{2}}$ dargestellt.

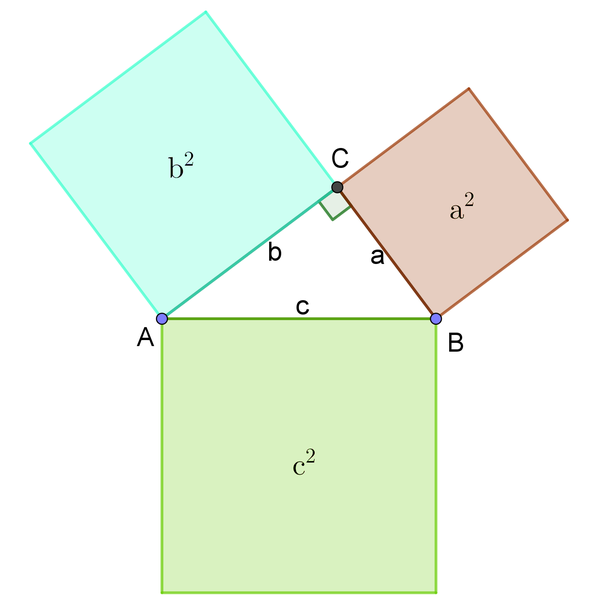
Du kannst schon nach Augenmaß vermuten, dass $\mathrm{a^{2}+b^{2}=c^{2}}$ gilt. In Worten: In einem rechtwinkligen Dreieck ist die Summe der Flächeninhalte der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrats.

Für den Satz des Pythagoras gibt es über 400 Beweise. Er gilt damit als der meistbewiesene Satz. Jetzt folgt ein einfacher geometrischer Beweis:

Zeichne dazu zunächst die untere Beweisfigur nach. Benutze z. B. folgende Längen: $\mathrm{a=4\,cm}$ und $\mathrm{b=3\,cm}$.

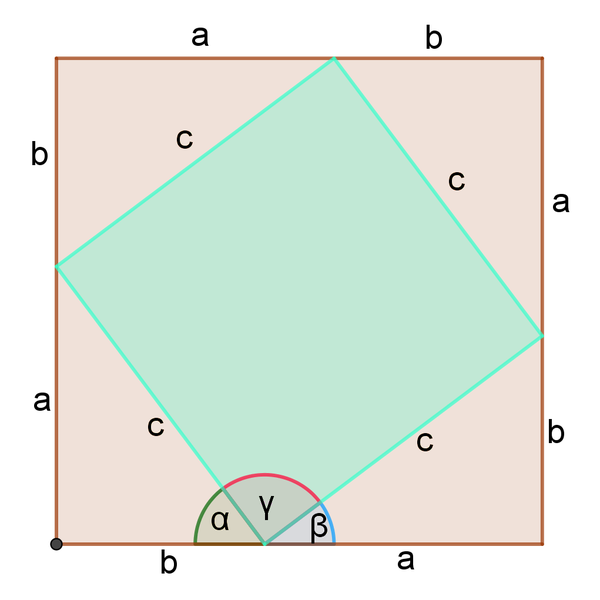
Das große Quadrat hat eine Seitenlänge von $\mathrm{a+b}$ und damit einen Flächeninhalt von $\mathrm{(a+b)^{2}=a^{2}+2⋅a⋅b+b^{2}}$. Es gibt noch eine weitere Möglichkeit, den Flächninhalt zu berechnen: Das große Quadrat setzt sich aus der blauen Raute mit der Länge c und vier rechtwinkligen Dreiecken mit den Katheten a und b und der Hypotenuse c zusammen.

Jetzt wird gezeigt, dass die Raute sogar ein Quadrat ist: Für die Winkelsumme in den rechtwinkligen Dreiecken gilt jeweils $\mathrm{α+β+90°=180°}$. Also gilt: $\mathrm{α+β=90°}$. Weiter gilt (siehe Beweisfigur): $\mathrm{α+β+γ=180°}$, denn die drei Winkel bilden einen gestreckten Winkel. Also folgt: $\mathrm{90°+γ=180°}$ und schließlich $\mathrm{γ=90°}$. Wenn ein Winkel einer Raute 90° groß ist, dann sind alle Winkel 90° groß. Die Raute ist also ein Quadrat mit der Seitenlänge c.

Nun kann man den Flächeninhalt des großen Quadrats auch wie folgt ausrechnen: $\mathrm{4⋅A_{rechtwinklige Dreiecke}+A_{blaues Quadrat}=4⋅\frac{a⋅b}{2}+c^{2}=2⋅a⋅b+c^{2}}$.

Beide Formeln für den Flächeninhalt des großen Quadrats werden jetzt gleichgesetzt:

$\mathrm{a^{2}+2⋅a⋅b+b^{2}=2⋅a⋅b+c^{2}\quad|-2⋅a⋅b}$

$\mathrm{a^{2}+b^{2}=c^{2}}$. Das sollte bewiesen werden. Der Beweis ist jetzt abgeschlossen.

Es gilt sogar die Umkehrung: Wenn in einem Dreieck $\mathrm{a^{2}+b^{2}=c^{2}}$ gilt, dann ist das Dreieck rechtwinklig.

Es gibt zahlreiche Anwendungen für den Satz des Pythagoras.  Aber die Quadratur eines Rechtecks ist mit dem Satz des Pythagoras nicht möglich, da in $\mathrm{a^{2}+b^{2}=c^{2}}$ nur Quadrate und kein Rechteck mit verschiedenen Längen vorkommen. Der Satz des Pythagoras dient in diesem Lernpfad als Basis und Beweismittel für die folgenden Sätze, mit denen die Quadratur möglich ist.

Bevor du mit der Quadratur mittels Höhensatz beginnst, musst du wissen,  was der Höhensatz des Euklid aussagt. Dazu schaue dir das folgende Bild an:  

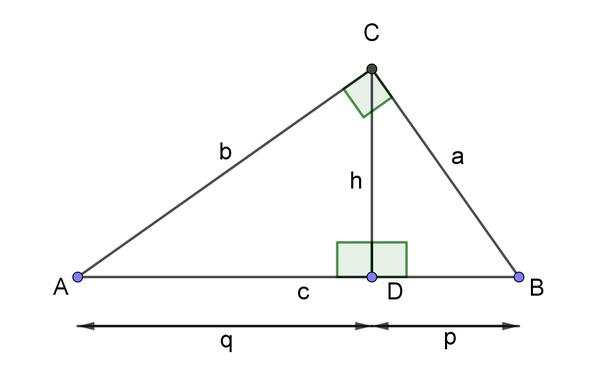
In einem rechtwinkligen Dreieck teilt die Höhe h durch den Punkt C auf die Hypotenuse c diese Seite in die zwei sogenannten Hypotenusenabschnitte q und p (q wird gewöhnlich links und p rechts gezeichnet). Der Höhensatz besagt nun, dass $\mathrm{h^{2}=p⋅q}$ ist. In Worten: In einem rechtwinkligen Dreieck ist das Quadrat über der Höhe genauso groß wie das Rechteck aus den beiden Hypotenusenabschnitten.

Das ist doch ein erstaunliches Ergebnis, das bewiesen werden muss (Es gibt viele Beweise für den Höhensatz. Der folgende Beweis ist einer der einfachen Beweise.):

Du darfst beim Beweis dreimal den Satz des Pythagoras anwenden, da die Höhe das große rechtwinklige Dreieck in zwei weitere kleinere rechtwinklige Dreiecke unterteilt (siehe das obige Bild. In diesem Bild ist der rechte Winkel statt mit einem Viertelkreis mit einem Punkt mit einem kleinen Quadrat gekennzeichnet. Auch das ist eine übliche Darstellung für einen rechten Winkel.):

Für das große rechtwinklige Dreieck ABC gilt: $\mathrm{a^{2}+b^{2}=c^{2}}$

Für das rechtwinklige Dreieck ADC gilt: $\mathrm{q^{2}+h^{2}=b^{2}}$

Für das rechtwinklige Dreieck CDB gilt: $\mathrm{h^{2}+p^{2}=a^{2}}$

Es gilt auch: $\mathrm{q+p=c}$

Setze jetzt in die erste Gleichung die Informationen der anderen Gleichungen ein, um schließlich eine Gleichung zu erhalten, die nur noch h, p und q enthält:

$\mathrm{a^{2}+b^{2}=c^{2}\,\Leftrightarrow}$

$\mathrm{h^{2}+p^{2}+q^{2}+h^{2}=(q+p)^{2}\,\Leftrightarrow}$

$\mathrm{2⋅h^{2}+p^{2}+q^{2}=q^{2}+2⋅p⋅q+p^{2}\quad|-q^{2}-p^{2}}$

$\mathrm{2⋅h^{2}=2⋅p⋅q\quad|:2}$

$\mathrm{h^{2}=p⋅q}$. Du erhältst genau die Gleichung, die du beweisen solltest. Also bist du mit dem Beweis fertig.

Jetzt ist es endlich soweit: Das folgende Bild zeigt dir, wie man ein flächengleiches Quadrat von einem gegebenem Rechteck mit dem Höhensatz konstruiert.

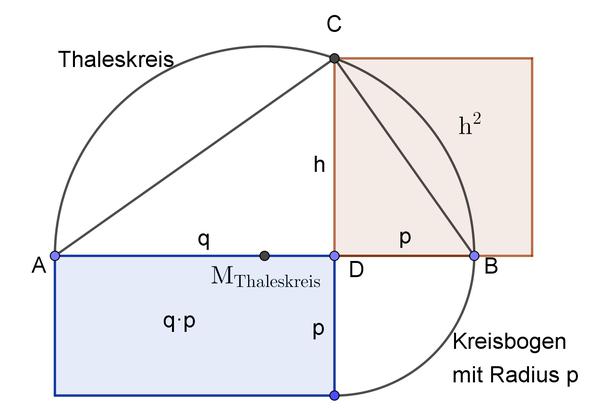
Konstruktionsbeschreibung: Zeichne ein Rechteck mit den Längen $\mathrm{q=\overline{AD}=6\,cm}$ und $\mathrm{p=3\,cm}$. Zeichne einen Kreisbogen um D mit dem Radius p und verlängere q so, dass sich die Verlängerung mit dem Kreisbogen schneidet. Nenne den Schnittpunkt B. Konstruiere nun den Thaleskreis über die Strecke $\mathrm{\overline{AB}}$ (siehe Vorwissen). Verlängere jetzt p so, dass sich die Verlängerung mit dem Thaleskreis schneidet. Nenne den Schnittpunkt C. Die Strecke $\mathrm{\overline{CD}=h}$ ist die gesuchte Quadratseite. Zeichne schließlich das Quadrat $\mathrm{h^{2}}$.

Gratulation, du hast es geschafft. Du kannst auch überprüfen, ob deine Konstruktion richtig ist, indem du die Länge von h mißt: Das Rechteck hat den Flächeninhalt von $\mathrm{6\,cm⋅3\,cm=18\,cm^{2}}$. Also hat h die Länge von $\mathrm{\sqrt{18\,cm^{2}}≈4,2\,cm}$.

Es gibt noch eine zweite Möglichkeit für die Quadratur eines Rechtecks, nämlich die Quadratur mittels Kathetensatz. Zunächst musst du wissen, was der Kathetensatz des Euklid aussagt. Dazu schaue dir das folgende Bild an:

Bezüglich des Kathetensatzes musst du dir zwei Formeln merken:

• $\mathrm{a^{2}=p⋅c}$
• $\mathrm{b^{2}=q⋅c}$

In Worten: Das Quadrat über die Kathete a bzw. b ist flächeninhaltsgleich zum Rechteck mit dem anliegenden Hypotenusenabschnitt p bzw. q und der Hypotenuse c.

Für den Beweis benötigst du nur einmal den Satz des Pythagoras, den Höhensatz des Euklid $\mathrm{h^{2}=p⋅q}$ und die Gleichung $\mathrm{c=p+q}$. Beginne mit dem Beweis von $\mathrm{a^{2}=p⋅c}$:

Gemäß des Satzes des Pythagoras gilt im rechtwinkligen Dreieck CDB (siehe obiges Bild):

$\mathrm{a^{2}=h^{2}+p^{2}}\Leftrightarrow$

$\mathrm{a^{2}=p⋅q+p^{2}}\Leftrightarrow$

$\mathrm{a^{2}=p⋅(q+p)}\Leftrightarrow$

$\mathrm{a^{2}=p⋅c}$. Schon bist du fertig.

Der Beweis zu $\mathrm{b^{2}=q⋅c}$ ist analog. Du musst nur mit $\mathrm{b^{2}=h^{2}+q^{2}}$ beginnen.

Jetzt ist es endlich wieder soweit: Das folgende Bild zeigt dir, wie man ein flächengleiches Quadrat von einem gegebenem Rechteck mit dem Kathetensatz konstruiert:

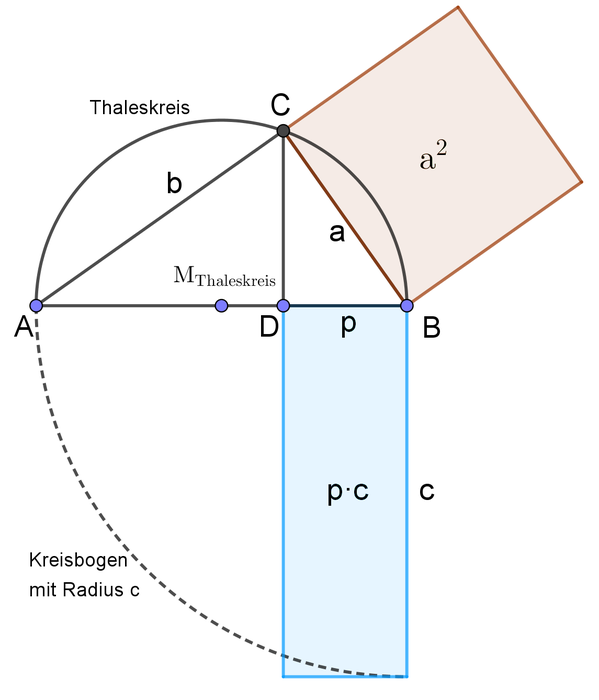
Konstruktionsbeschreibung: Zeichne ein Rechteck mit den Seitenlängen $\mathrm{p=\overline{DB}=2\,cm}$ und $\mathrm{c=6\,cm}$. Zeichne einen Kreisbogen um B mit dem Radius c nach links. Verlängere p so, dass sich die Verlängerung mit dem Kreisbogen schneidet. Nenne den Schnittpunkt A. Konstruiere jetzt den Thaleskreis über $\mathrm{\overline{AB}}$. Verlängere die linke Seite des Rechtecks so, dass sie sich mit dem Thaleskreis schneidet. Nenne den Schnittpunkt C. Die Strecke $\mathrm{\overline{CB}}$ ist die gesuchte Quadratlänge. Zeichne schließlich das Quadrat $\mathrm{a^{2}}$.

Bei dieser Konstruktion wurde die Variante $\mathrm{a^{2}=c⋅p}$ des Kathetensatzes benutzt. Analog kannst du auch die Variante $\mathrm{b^{2}=c⋅q}$ benutzen.

Gratulation, du hast auch diese Quadratur geschafft. Du kannst auch überprüfen, ob deine Konstruktion richtig ist, indem du die Länge von a mißt: Das Rechteck hat den Flächeninhalt von $\mathrm{6\,cm⋅2\,cm=12\,cm^{2}}$, also hat a die Länge von $\mathrm{\sqrt{12\,cm^{2}}≈3,5\,cm}$ .

Formuliere als Formel und in Worten den Satz des Pythagoras!

Beweise den Satz des Pythagoras mit Beweisfigur!

Formuliere als Formel und in Worten den Höhensatz des Euklid!

Beweise den Höhensatz des Euklid mit Beweisfigur!

Formuliere als Formel und in Worten den Kathetensatz des Euklid!

Beweise den Kathetensatz des Euklid mit Beweisfigur!

Konstruiere ein flächeninhaltsgleiches Quadrat aus einem Rechteck mit den Längen 3 cm und 4 cm sowohl mit dem Höhensatz als auch mit dem Kathetensatz! Kontrolliere dein Ergebnis durch eine Rechnung!

Konstruiere ein flächeninhaltsgleiches Quadrat aus einem Rechteck mit den Längen 8 cm und 2 cm sowohl mit dem Höhensatz als auch mit dem Kathetensatz! Kontrolliere dein Ergebnis durch eine Rechnung!

Die Lösungen findest du in den entsprechenden Reitern.