Der Blick in die Ferne: Fernrohre und Spiegelteleskope
- Vorwissen
- Geschichte
- Kepler-Fernrohr
- Feldstecher
- Galilei-Fernrohr
- Spiegelteleskop
- große Teleskope
- Vertiefung
- Teste dein Wissen I
- Teste dein Wissen II
Vorwissen
Was musst du wissen?
Liebe Schülerin und lieber Schüler,
um die Funktionsweise von Fernrohren und Spiegelteleskopen verstehen zu können, musst du Folgendes wissen:
Was sind Sammellinsen, auch Konvexlinsen genannt, und was sind Zerstreuungslinsen, auch Konkavlinsen genannt?
Die Begriffe Brennweite, Brennpunkt, optische Achse, Mittelebene, Parallelstrahl, Mittelpunktsstrahl und Brennstrahl musst du kennen.
Wie konstruiert man das Bild bei einer Sammellinse? Dabei hilft dir das folgende Bild:
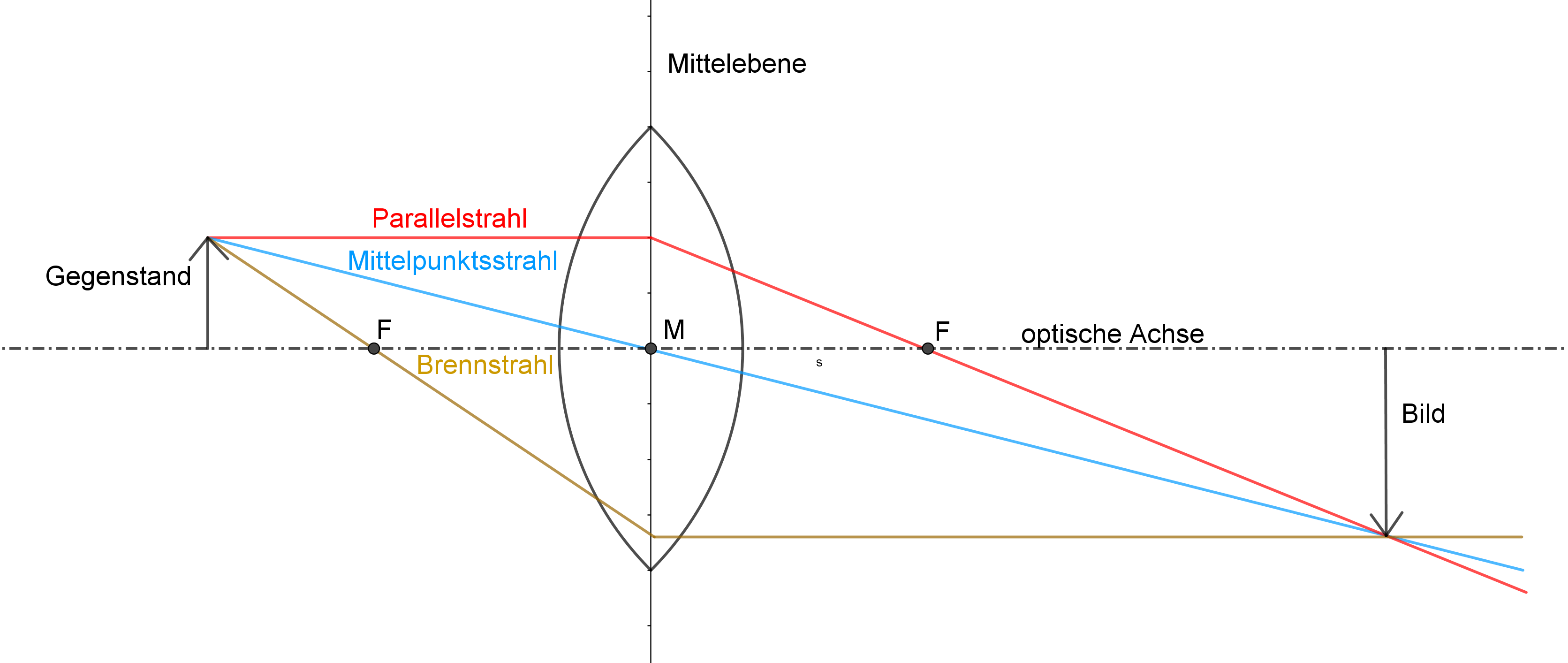
Du musst auch den Unterschied zwischen einem reellen und einem virtuellen Bild kennen.
Sehr gut solltest du wissen, wie eine Lupe und die Totalreflexion funktioniert.
Wie konstruiert man das virtuelle Bild bei einer Zerstreuungslinse? Dabei hilft dir das folgende Bild:
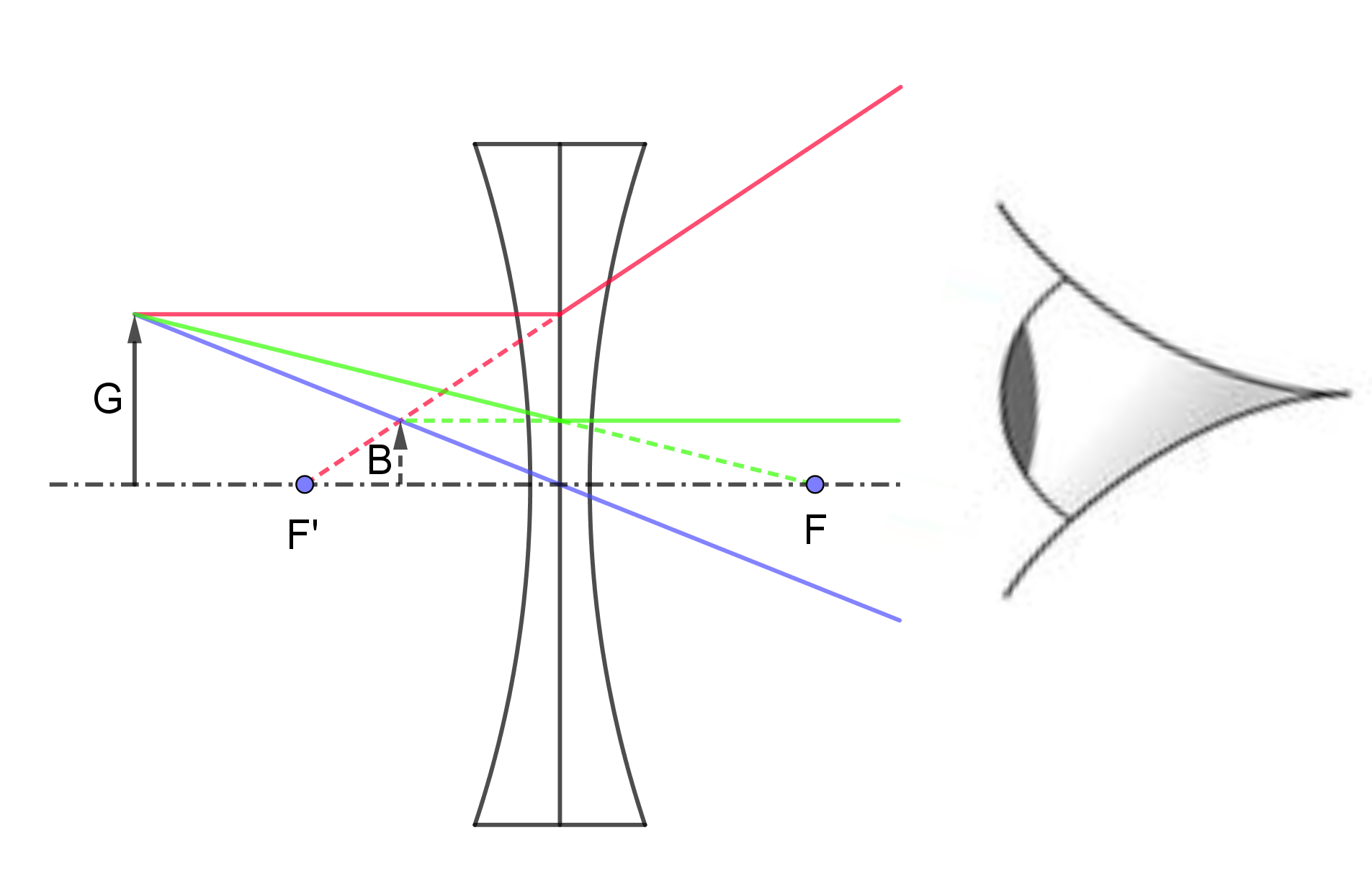
Auch solltest du wissen, was die Ursachen für Abbildungsfehler sind und wie man sie beheben kann. Die Fachbegriffe dazu sind sphärische und chromatische Abberation.
Geschichte
Seit wann gibt es Fernrohre und wer hat's erfunden?

Astronomie wurde schon in den ersten Hochkulturen betrieben. Aber erst im Jahr 1608 gelang es dem Holländischen Brillenmacher Hans Lipperhey, das erste sogenannte Holländische Fernrohr zu konstruieren. Damals befand sich die aufstrebende Niederlande im Unabhängigkeitskrieg mit Spanien und ein Fernrohr war von großer militärischer Bedeutung. Seit über ca. 400 Jahren gibt es also Fernrohre und ein Holländer war sein Erfinder.
Beim Holländischen Fernrohr ist das objektseitige Objektiv eine langbrennweitige Sammellinse und das augenseitige Okular ist eine kurzbrennweitige Zerstreuungslinse. Die Funktionsweise wird dir später erklärt.

Im Jahr 1609 konstruierte Galileo Galilei (Porträt siehe oben) nach dem Holländischem Vorbild ein verbessertes Fernrohr. Mit seinem Fernrohr machte er für die damalige Zeit spektakuläre Entdeckungen. Er beobachtete als erster Mensch die vier hellen Jupitermonde, die Ringe des Saturn, die Mondgebirge, die Sonnenflecken und die Auflösung der Milchstraße in viele schwache Sterne. Das Holländische Fernrohr nennt man zu Ehren Galileis auch Galilei-Fernrohr.
1611 konstruierte Johannes Kepler ein Fernrohr, bei dem auch das Okular eine kurzbrennweitige Sammellinse ist. Fernrohre mit dieser Bauweise nennt man Kepler-Fernrohre. Die Funktionsweise wird dir später erklärt.

1668-1672 entwickelte Isaac Newton (Porträt siehe oben) ein Spiegelteleskop mit einem kleinen Fangspiegel in der optischen Achse des Hauptspiegels, über den man seitlich in das Gerät hineinblicken konnte. Diese Bauweise wird heute noch wegen ihres einfachen Aufbaus genutzt.
1672 wurde von dem französischen Gelehrten Laurent Cassegrain eine neue Bauart für Spiegelteleskope konstruiert. Das Licht des konkaven Hauptspiegels wird dabei auf einen Fangspiegel reflektiert, der leicht konvex ist und das Licht zum durchbohrten Hauptspiegel zurück bündelt.
Die weitere Entwicklung wird unter dem Reiter "große Teleskope" beschrieben.
Kepler-Fernrohr
Wie funktioniert das Kepler-Fernrohr?
Zunächst wird dir erklärt, wie das Kepler-Fernrohr, auch astronomisches Fernrohr genannt, funktioniert. Es wurde zwar später als das Galilei-Fernrohr konstruiert (siehe Reiter Geschichte), aber die Funktionsweise ist beim Kepler-Fernrohr leichter zu verstehen. In der folgenden Darstellung wird das Bild eines weit entfernten Gegenstands mittels des Kepler-Fernrohrs konstruiert:
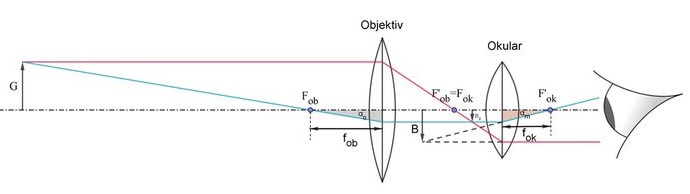
Ganz allgemein formuliert, musst du dir Folgendes merken:
Das Objektiv erzeugt von einem fernen Gegenstand ein reelles Zwischenbild. Dieses wird durch das Okular wie mit einer Lupe betrachtet.
Da du unbedingt die Konstruktion verstehen und nachzeichnen solltest, folgt eine ausführliche Konstruktionsbeschreibung:
Nehme ein DIN A4 Blatt quer. Beginne mit dem Zeichnen der strichpunktierten optischen Achse. Zeichne möglichst am linken Rand einen 2 cm hohen Pfeil. Dieser Pfeil ist der Gegenstand. 15 cm weiter nach rechts zeichne die Mittelebene der Objektivlinse mit der Brennweite $f_{ob} = 3\ cm$. Zeichne die Brennpunkte $F_{ob}$ und $F'_{ob}$. 5 cm von der Mittelebene der Objektivlinse entfernt zeichne die Mittelebene der Okularlinse mit der Brennweite $f_{ok} = 2\ cm$. Zeichne die Brennpunkte $F_{ok}$ und $F'_{ok}$. Dabei stellst du fest, dass $F'_{ob}$ und $F_{ok}$ zusammenfallen. Ganz rechts zeichne ein Auge ein. Jetzt beginnt die eigentliche Konstruktion des Bildes: Beginne mit dem roten Lichtstrahl: Er verläuft zunächst parallel zur optischen Achse, er wird vom Objektiv so gebrochen, dass er durch den Brennpunkt $F'_{ob}$ läuft. Da die Brennpunkte $F'_{ob}$ und $F_{ok}$ zusammenfallen, verläuft der Strahl nach der Brechung durch das Okular wieder parallel zur optischen Achse. Der hellblaue Lichtstrahl geht zunächst durch den Brennpunkt $F_{ob}$ und wird vom Objektiv so gebrochen, dass er parallel zur optischen Achse läuft. Dort, wo sich der rote und der hellblaue Strahl schneiden, entsteht das reelle Zwischenbild $B_{z}$ der Pfeilspitze. Das Zwischenbild des Pfeils ist also verkleinert, reell, auf dem Kopf stehend und seitenverkehrt. Der hellblaue Strahl wird schließlich so durch das Okular gebrochen, dass er durch den Brennpunkt $F'_{ok}$ läuft. Es entsteht also insgesamt ein divergentes Lichtbündel mit dem hellblauen und roten Strahl als Randstrahlen, das ins Auge gelangt. Unser menschliches Auge geht immer von einer geradlinigen Lichtausbreitung aus, so dass der hellblaue und der rote Strahl nach links verlängert werden (siehe die gestrichelten Linien in der obigen Darstellung). Dort, wo sich die gestrichelten Linien schneiden, entsteht schließlich das virtuelle Bild B der Pfeilspitze. Insgesamt entsteht ein virtuelles, verkleinertes, auf den Kopf stehendes und seitenverkehrtes Bild des Pfeils. Gratulation, du hast die Konstruktion geschafft. Wenn dir nicht gleich alles beim ersten Mal gelungen ist, dann führe die Konstruktion ein zweites Mal durch. Je mehr du übst, desto sicherer und schneller wirst du bei der Bildkonstruktion.
Du freust dich bestimmt über deine gelungene Konstruktion, aber du bist sicher enttäuscht von dem Ergebnis: Der ganze Aufwand nur für ein verkleinertes und virtuelles Bild!!! Das stimmt zwar, aber schaue genauer auf die obige Darstellung: Der Sehwinkel, unter dem man ein Objekt sieht, und er spielt hier die Hauptrolle, hat sich von $α_{o}$ (o wie ohne Gerät) auf $α_{m}$ (m wie mit Gerät) vergrößert. Der Sehwinkel bestimmt nämlich die Größe des Nethautbildes.
In der folgenden Darstellung ist die Bildentstehung bei einem unendlich weit entfernten Objekt wie z. B. bei einem Stern mit schräg einfallenden zueinander parallelen Strahlen dargestellt:
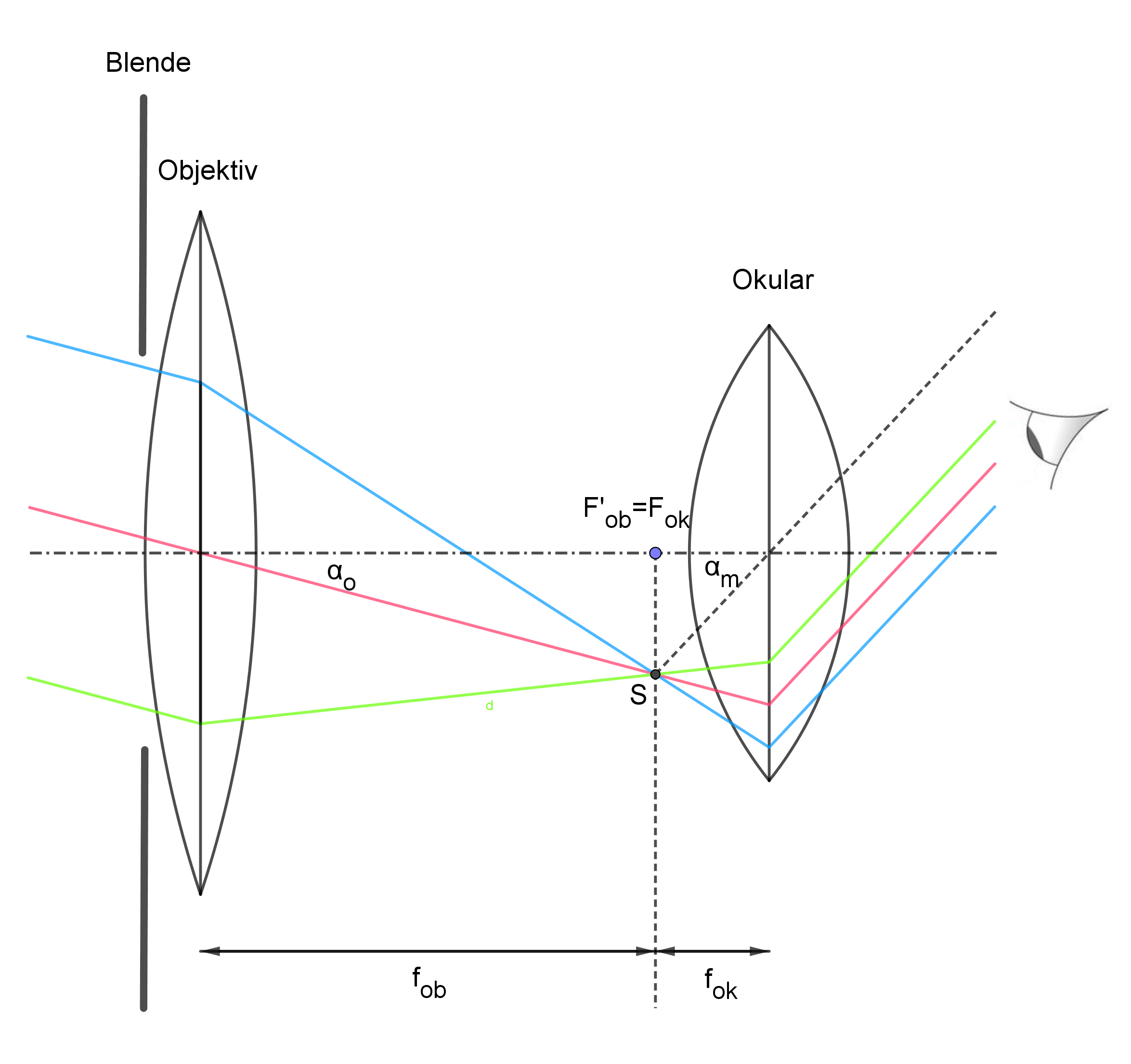
Du erkennst, dass die zueinander parallel einfallenden Strahlen auch nach dem Durchgang durch das Fernrohr parallel ins Auge gelangen und sich dabei der Sehwinkel deutlich vergrößert hat.
Die Vergrößerung kann man sogar berechnen: Dazu schaue dir die obigen Darstellungen genau an. Du erkennst, dass $α_{o}$ dem Verhältnis $\frac{B_{z}}{f_{ob}}$ und $α_{m}$ dem Verhältnis $\frac{B_{z}}{f_{ok}}$ entspricht. Also beträgt die Winkelvergrößerung $V=\frac{α_{m}}{α_{o}}=\frac{\frac{B_{z}}{f_{ok}}}{\frac{B_{z}}{f_{ob}}}=\frac{B_{z}}{f_{ok}}⋅\frac{f_{ob}}{B_{z}}=\frac{f_{ob}}{f_{ok}}$. Die Fernrohrlänge ist leichter zu berechnen: Da $F'_{ob}$ und $F_{ok}$ zusammenfallen, beträgt der Abstand des Objektivs zum Okular $f_{ob}+f_{ok}$ und das ist auch die Fernrohrlänge. Merke also:
Die Vergrößerung eines Kepler-Fernrohrs beträgt $V=\frac{f_{ob}}{f_{ok}}$ und die Länge beträgt $l=f_{ob}+f_{ok}$.
Um die chromatische und sphärische Abberation zu verhindern, besteht sowohl das Objektiv als auch das Okular aus Linsensystemen. Des Weiteren ist darauf zu achten, dass die Objektivlinse genügend groß ist, damit genügend Licht in das Fernrohr eindringen kann. Mit einem guten Stativ und einem Suchfernrohr ausgestattet, ist das astronomische Fernrohr nun fertig. Wie man das Kepler-Fernrohr auch für Beobachtungen auf der Erde einsetzen kann, erfährst du unter dem nächsten Reiter.
Feldstecher
Wie funktioniert der Feldstecher?

Für astronomische Beobachtungen stört es nicht, dass das Bild eines Sterns auf dem Kopf steht und rechts und links vertauscht sind. Möchte man das Kepler-Fernrohr auch für Beobachtungen auf der Erde nutzen, muss man dafür sorgen, dass das Bild aufrecht steht und seitenrichtig ist. Das kann man mit folgenden Techniken erreichen:
Man baut eine zusätzliche Linse als Umkehrlinse ein. Das hat den großen Nachteil, dass das Fernrohr länger wird: $l=f_{ob}+f_{ok}+4⋅f_{umkehr}$.
Viel eleganter ist folgende Lösung, die auch in den sogenannten Feldstechern oder Prismenfernrohren (siehe Bild oben) genutzt wird: Man baut zwei Prismen zwischen Objektiv und Okular ein (siehe Bild unten). Ein Prisma vertauscht bei der Totalreflexion des Lichts an seinen Seitenflächen rechts und links, das andere vertauscht obern und unten. So entsteht insgesamt ein aufrechtes und seitenrichtiges Bild. Des Weiteren wird dadurch der Strahlengang "gefaltet" und der Feldstecher verkürzt.
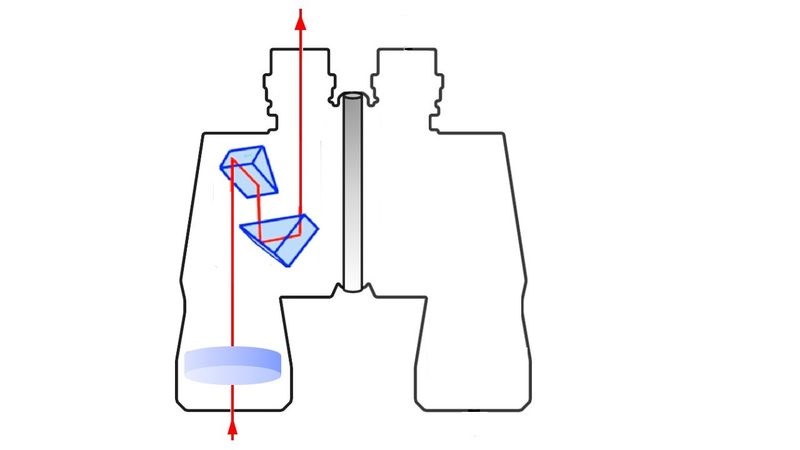
Anhand der oberen Bilder erkennst du, dass die Feldstecher "zweiäugig" gebaut sind. Der Fachbegriff dafür lautet "binokular". Des Weiteren erkennst du, dass die Objektive weiter auseinander liegen als die Okulare. Das sorgt für besonders plastische Bilder.
Galilei-Fernrohr
Wie funktioniert das Galilei-Fernrohr?

In diesem Reiter wird dir das Holländische oder Galileische Fernrohr vorgestellt, das noch vor dem Kepler-Fernrohr (siehe Reiter Geschichte) entwickelt wurde. Es hat wie das Kepler-Fernrohr als Objektivlinse eine langbrennweitige Sammellinse, aber im Unterschied zum Kepler-Fernrohr ist die Okularlinse eine kurzbrennweitige Zerstreuungslinse. Die Brennpunkte von Objektiv und Okular fallen auf der Beobachterseite zusammen, also: $F'_{ob}=F_{ok}$. In der folgenden Darstellung ist die Bildentstehung eines weit entfernten Gegenstandes dargestellt:
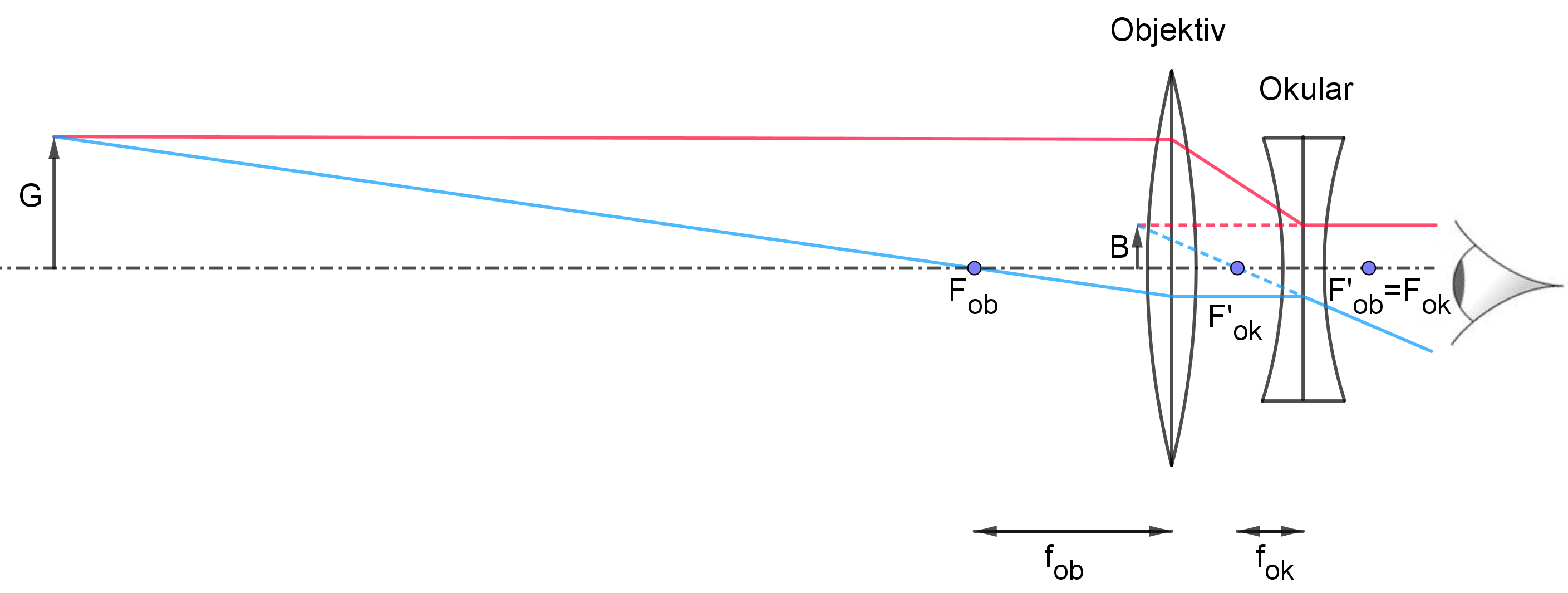
Es entsteht ein virtuelles, verkleinertes, aufrechtes und seitenrichtiges Bild des Gegenstandes. Für Erdbeobachtungen ist das ein großer Vorteil. Man benötigt keine zusätzlichen Bauteile für die Bildumkehr. Allerdings ist das Sichtfeld viel kleiner als beim Kepler-Fernrohr. Auch beim Galilei-Fernrohr ist wie beim Kepler-Fernrohr $α_{m}$ größer als $α_{o}$.
Im unteren Bild ist die Bildkonstruktion mit schräg einfallenden zueinander parallelen Strahlen eines "unendlich" weit entfernten Sterns dargestellt:
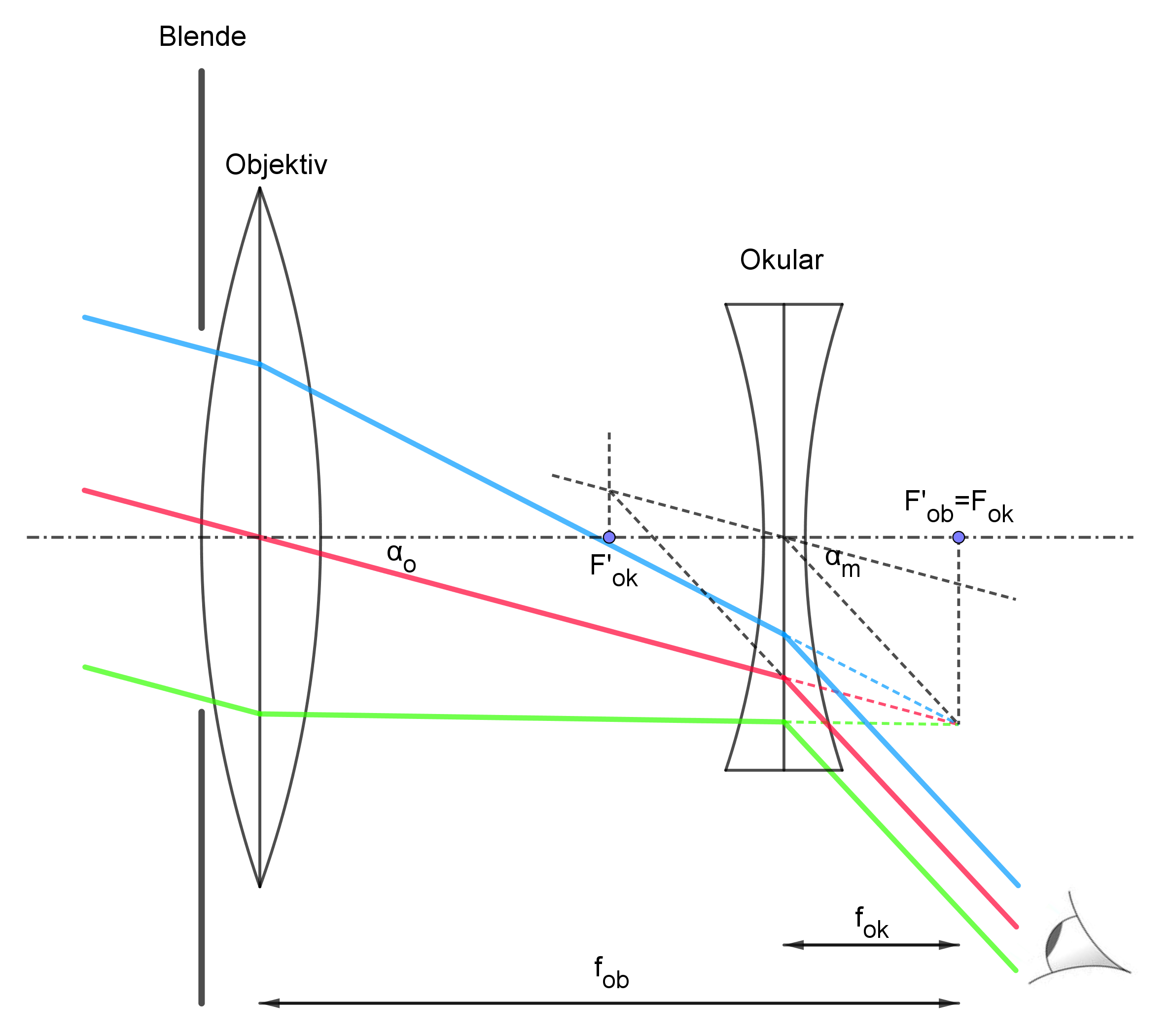
Merke Folgendes:
Die Vergrößerung eines Galilei-Fernrohrs beträgt $V=\frac{f_{ob}}{|f_{ok}|}$ und die Länge beträgt $l=f_{ob}-|f_{ok}|$.
Im obigen Merksatz steht $f_{ok}$ in Betragstrichen, da die Brennweite einer Zerstreuungslinse ein negatives Vorzeichen hat. Das Galilei-Fernrohr ist also kleiner als ein Kepler-Fernrohr mit gleicher Vergrößerung. Aber wegen des kleinen Sichtfeldes wird es heute weniger für astronomische Zwecke genutzt, sondern am häufigsten als Opernglas (siehe oben erstes Bild).
Spiegelteleskope
Wie sind Spiegelteleskope aufgebaut?
Die bisher beschriebenen Fernrohre wurden aus Linsen gebaut. Man nennt sie auch Refraktoren. Aber sie haben u. a. den großen Nachteil, dass das Fernrohrobjektiv, das wegen der Beobachtung lichtschwacher Objekte einen großen Durchmesser haben muss, ein hohes Gewicht hat. Aufgrund des hohen Gewichts biegt sich die Objektivlinse, die nur an den Rändern gestützt werden kann, durch. Dies führt zu unscharfen Bildern.
Deshalb hat Newton (siehe Reiter Geschichte) statt einer Linse einen Hohlspiegel als Objektiv benutzt (siehe Bild):
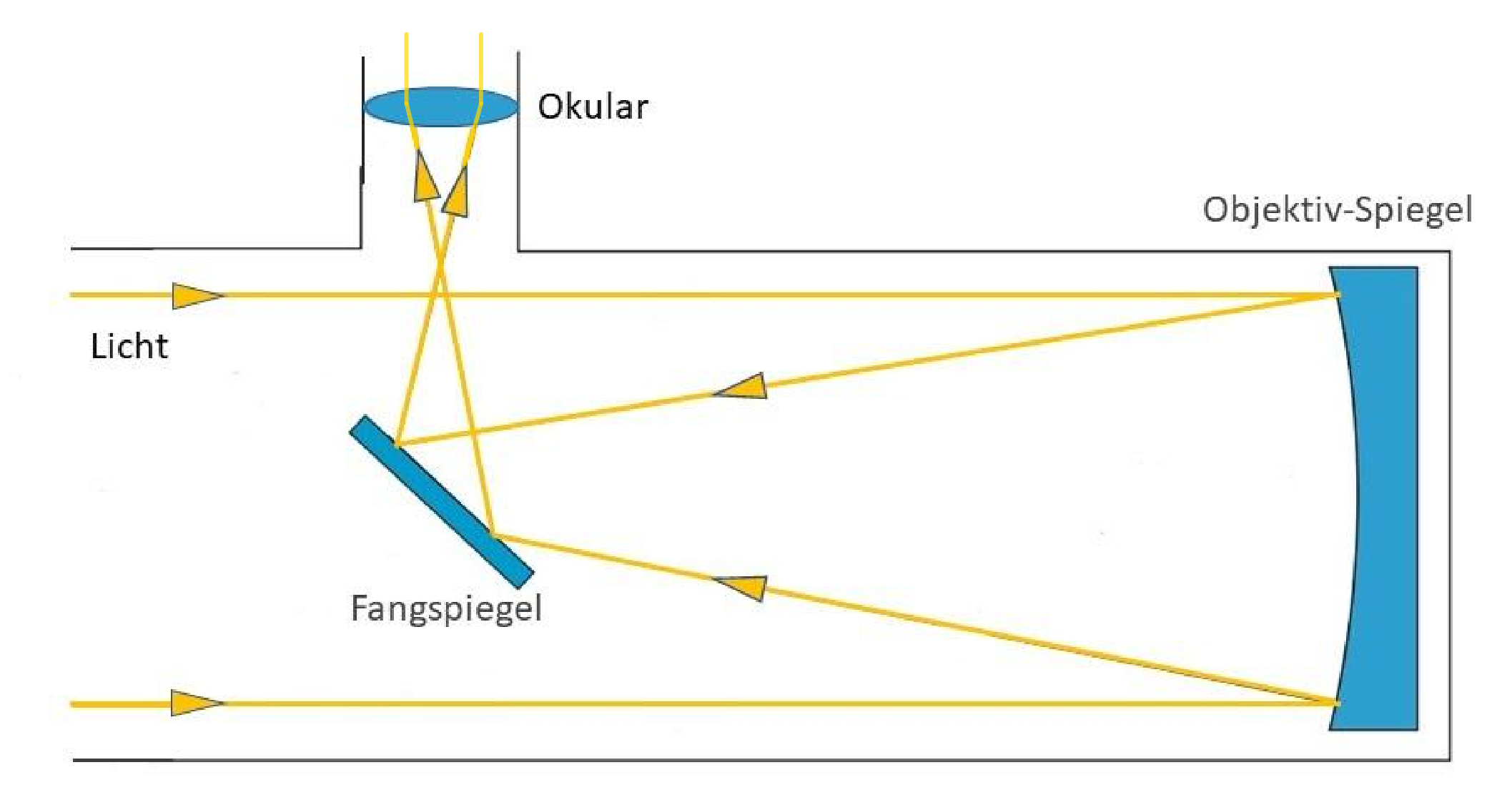
Das Zwischenbild liegt dabei vor dem Hohlspiegel und wird mit einem flachen und um 45° zur optischen Achse geneigten Fangspiegel zur Seite reflektiert, wo es mit einer Lupe betrachtet werden kann. Die Lichtverluste durch die Abschattung des Fangspiegels und seiner Halterung betragen nur ca. 7 %. Das nach Newton benannte Newtonteleskop wird heute noch häufig genutzt.
Eine weitere weit verbreitete Bauform eines Spiegelteleskops ist das Schmidt-Cassegrain-Teleskop (siehe Bild):
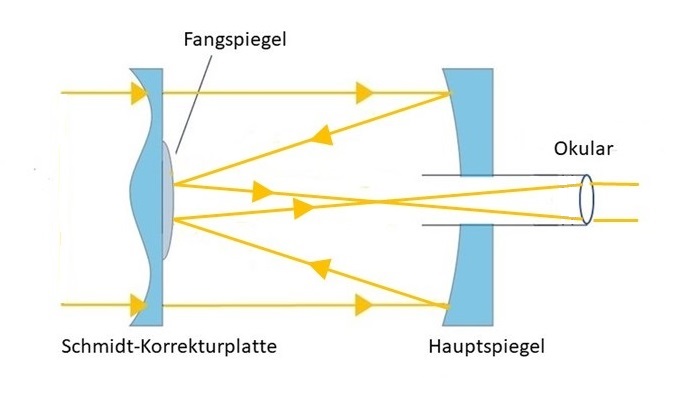
Der Objektivspiegel, auch Hauptspiegel oder Primärspiegel genannt, ist hier ein sphärischer Spiegel, der das Licht gebündelt zurückwirft. Ein konvex geschliffener Fangspiegel wirft das Licht wieder in Gegenrichtung zurück, wo es durch eine Öffnung im Hauptspiegel wieder nach außen tritt und mit einer Lupe betrachtet werden kann. Da der konvexe Fangspiegel den Strahlengang aufweitet, verlängert er die effektive Brennweite des Hauptspiegels. Dies führt zu einer kompakten Bauweise mit relativ großer Brennweite.
Die Abbildungsfehler des sphärischen Spiegels werden durch die Schmidt-Korrekturplatte beseitigt.
große Teleskope
Welche großen Teleskope gibt es heute?

Im Reiter Geschichte hast du gelernt, dass die ersten Linsenfernrohre und Spiegelteleskope im 17. Jhd. entwickelt wurden. Im 18. und 19. Jhd. entwickelte man aufbauend auf den Techniken des 17. Jhds. immer größere Linsenfernrohre und Spiegelteleskope. Die Entwicklung der Linsenfernrohre stieß schließlich um 1900 mit ca. 1 m Objektivdurchmesser an ihre Grenzen: Die großen Linsen, die nur an ihren Rändern gehalten werden können, verbogen sich unter ihrem eigenen Gewicht. Im 20. Jhd. begann deshalb endgültig der Siegeszug der Spiegelteleskope, da die Spiegel auf ihrer gesamten Fläche von hinten gestützt werden können. So kann man heute einzelne Spiegel mit bis zu 8 m Durchmesser bauen. Für die heutigen astronomischen Forschungsaufgaben reicht selbst dieser Durchmesser nicht mehr aus. Man benutzt deshalb folgende technische "Tricks", um den Durchmesser zu vergrößern:
- Der Hauptspiegel wird nicht aus einem Stück gefertigt, sondern aus wabenförmig aneinandergesetzten Teilspiegeln aufgebaut. Mit solchen Segmentspiegeln kann man größere Spiegeldurchmesser erreichen. Ein Beispiel für einen Facettenspiegel ist der des Keck-Observatoriums auf Hawai mit einem Durchmesser von 10 m (siehe Bild oben).
- Die zweite Möglichkeit besteht darin, Spiegel so auf Stützen zu lagern, dass man durch computergesteuerte Verschiebung der Stützen die Spiegelform jeweils optimieren kann. Man nennt das auch aktive Lagerung. Ein Beispiel für ein solche Technik ist das New Technology Telescope der Europäischen Südsternwarte in Chile mit einem Spiegeldurchmesser von 3,58 m.
- Die dritte Möglichkeit besteht in der optischen Kopplung von mehreren Spiegelteleskopen. Das wird z. B. mit dem Very Large Telescope der Europäischen Südsternwarte realisiert. Bei dieser Anlage können vier unabhängig voneinander arbeitende 8-m-Spiegel mit aktiver Lagerung so miteinander gekoppelt werden, dass sie dann wie ein 16-m-Spiegel wirken.
Die oben beschriebenen Teleskope hat man in großer Höhe gebaut, um die Abbildungsfehler durch die Luftunruhe in der Atmosphäre zu minimieren. Auch hat man darauf geachtet, möglichst weit weg von menschlichen Ansiedlungen zu bauen, um störendes Licht zu vermeiden. Das Hubble-Weltraumteleskop (siehe Bild) hat den großen Vorteil, dass die Atmosphäre nicht mehr stört.

Du hast bestimmt schon im Physikunterricht gelernt, dass sich Licht als elektromagnetische Welle beschreiben lässt. Das sichtbare Licht ist nur ein kleiner Ausschnitt eines sehr viel größeren Spektrums. An das sichtbare Licht schließt mit kürzeren Wellenlängen die Ultraviolett-, Röntgen- und die hochenergetische Gammastrahlung an. An das sichtbare Licht schließt sich auf der anderen Seite des Spektrums mit größeren Wellenlängen das infrarote Licht, Mikrowellen und Radiowellen an. Für jeden Bereich gibt es entsprechende Teleskope. Im unteren Bild siehst du z. B. das Radioteleskop Effelsberg in der Eifel.

Vertiefung
Was solltest du noch wissen als Hobby-Astronom?
Eine weitere Formel für die Vergrößerung:
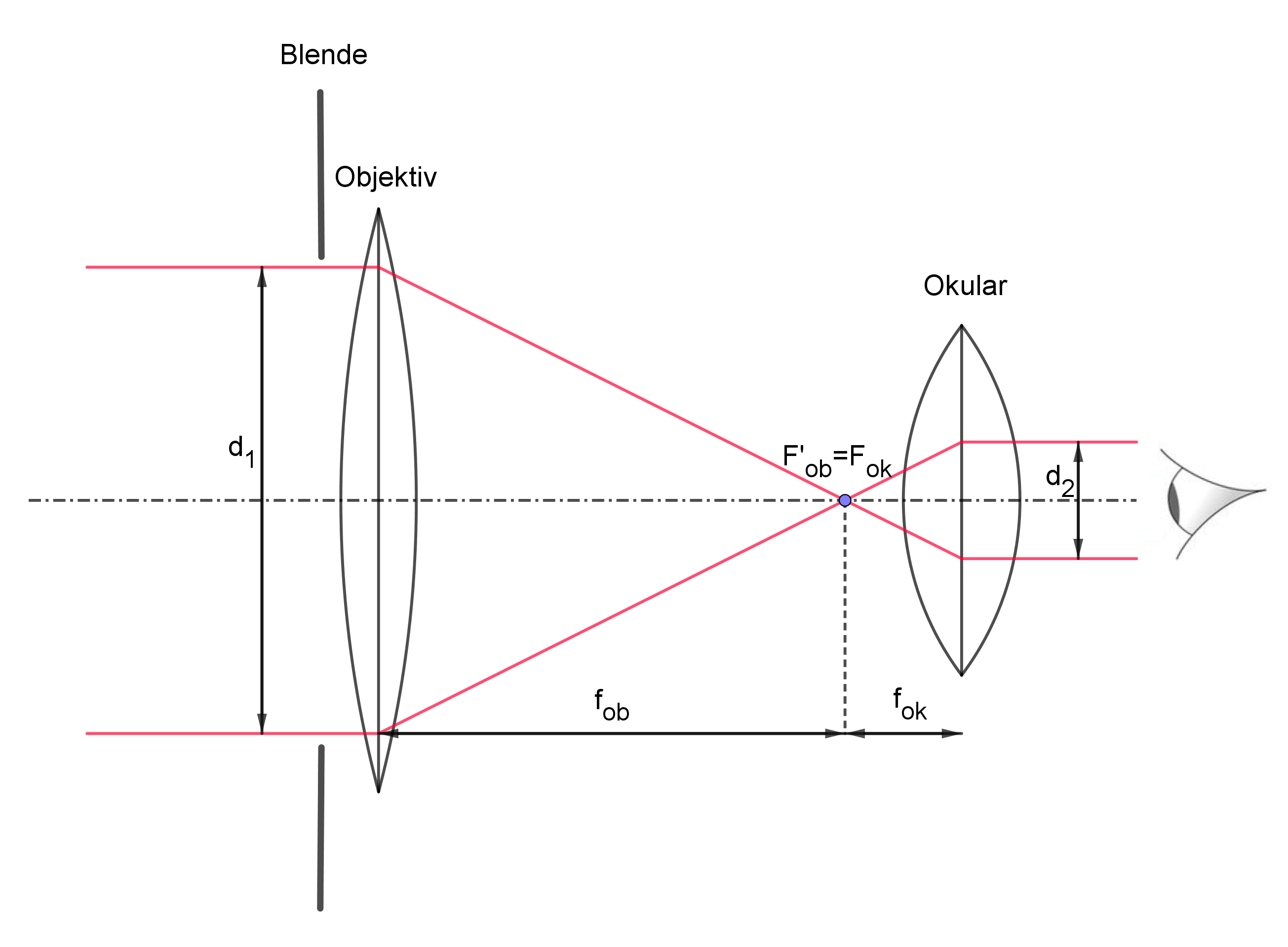
Im oberen Bild siehst du den Durchmesser $d_{1}$ der Objektivöffnung, auch Eintrittspupille genannt, und das Bild $d_{2}$ der Objektivöffnung, auch Austrittspupille genannt. Nach dem Strahlensatz ergibt sich: $\frac{d_{1}}{d_{2}}=\frac{f_{ob}}{f_{ok}}=V$. Damit gibt es eine zweite Möglichkeit, die Vergrößerung zu berechnen, die im Folgenden noch benutzt wird.
Wie groß sollte der Objektivdurchmesser sein?
Im oberen Bild begrenzen die roten Linien den Verlauf eines Lichtbündels, das achsenparallel auf das Objektiv fällt. Das Lichtbündel wird dabei vom Durchmesser $d_{1}$ auf den kleineren Durchmesser $d_{2}$ konzentriert. Die Pupille des Auges hat im Hellen einen Durchmesser von ca. 3 mm. Es reicht also aus, wenn ein aus dem Okular kommendes Parallelbündel den Durchmesser $d_{2} = 3\ mm$ hat, denn mehr Licht kann nicht ins Auge gelangen. Gemäß der obigen neuen Gleichung für die Vergrößerung wird das vom Feldstecher aufgefangene Licht dann optimal genutzt, wenn der Durchmesser des Objektivs $d_{1} = V⋅d_{2}$ beträgt. Vergrößert ein Feldstecher z. B. zehnmal, so ist ein Objektivdurchmesser von $d_{1}=10⋅3\ mm = 30\ mm$ optimal. In der Nacht weitet sich die Augenpupille auf ca. 7 mm. Bei zehnfacher Vergrößerung ist also im Dunklen ein Objektivdurchmesser von $d_{1} = 10⋅7\ mm = 70\ mm$ optimal.
Welche Angaben sind auf einem Feldstecher vermerkt?
Auf den Feldstechern sind die Vergrößerung und der Objektivdurchmesser angegeben. Die Angabe "10 x 42" z. B. bedeutet: Die Vergrößerung ist zehnfach und der Objektivdurchmesser beträgt 42 mm.
Sieht man eine Landschaft mit dem Feldstecher größer oder heller?
Das Objektiv eines Feldstechers fängt viel mehr Licht ein als das bloße Auge. Nach dem obigen Bild wird nämlich die Energie eines breiten Lichtbündels vom Okular auf einen kleineren Querschnitt konzentriert, so dass sie durch die Pupille ins Auge gelangen kann. Wird dadurch das Netzhautbild heller als mit bloßem Auge? Das ist nicht der Fall: Der Durchmesser des optimal aufzufangenden Lichtbündels wird zwar vom Feldstecher im Verhältnis $\frac{d_{1}}{d_{2}}$ erweitert, im gleichen Verhältnis vergrößert sich aber auch die Höhe des Netzhautbildes. Das Licht verteilt sich somit auf eine größere Fläche, dabei erhält die einzelne Sehzelle genauso viel Energie wie mit bloßem Auge. Man sieht also eine Landschaft mit dem Feldstecher größer, aber nicht heller.
Sieht man einen Fixstern mit dem Fernrohr größer oder heller?
Ein Fixstern ist so weit entfernt, dass selbst das stärkste Fernrohr davon nur ein Netzhautbild erzeugt, das nicht einmal eine einzige Sehzelle überdeckt. Deshalb sieht man einen Fixstern auch im Fernrohr nur als Punkt, der nicht größer als bei der Betrachtung mit bloßem Auge ist. Die vom Objektiv aufgefangene vermehrte Lichtenergie bleibt trotz der Vergrößerung immer noch auf eine Sehzelle begrenzt. Diese erhält dadurch mehr Licht. Einen Fixstern sieht man mit dem Fernrohr heller, aber nicht größer.
Wie muss ein Fernrohr montiert werden?
Ohne ein gutes Stativ mit entsprechender Montierung kann man mit dem Fernrohr nicht beobachten. Die Montierung soll folgende Aufgaben erfüllen:
- das Fernrohr zu tragen und es auf ein gewünschtes Himmelsobjekt zu richten.
- die Erddrehung zu kompensieren. Die Nachführung des Fernrohrs kann von Hand oder durch einen Motor erfolgen.
- Beobachtungsobjekte, die sich relativ zum Sternhintergrund merklich bewegen (z. B. Kometen), genau zu verfolgen.
Um die obigen Aufgaben zu erfüllen, gibt es zwei Möglichkeiten:
- Die azimutale Montierung ist die einfachste Art der Fernrohrmontierung, bei der sich das Fernrohr um eine vertikale sogenannte Stehachse und eine horizontale sogenannte Kippachse in alle Richtungen schwenken lässt.
- Die Alternative ist die äquatoriale Montierung, bei der die Primärachse nicht vertikal, sondern parallel zur Erdachse ausgerichtet ist.
Beide Montierungsmöglichkeiten haben ihre Vor- und Nachteile.
Kreuzworträtsel zum Vorwissen
Kreuzworträtsel
| virtuelle | Bilder die nicht auf einem Schirm aufgefangen werden können sind ... Bilder |
| Abberation | Lateinischer Begriff für Abbildungsfehler |
| Totalreflexion | Das komplette Licht wird am Übergang zwischen zwei Medien reflektiert. |
| optische | Die strichpunktierte Linie bei Bildkonstruktionen mit Linsen ist die ... Achse. |
| Brennweite | Abstand zwischen dem Mittelpunkt einer Linse und dem Brennpunkt der Linse |
| Konvexlinse | Lateinischer Begriff für Sammellinse |
| reelle | Bilder von denen wirklich Lichtstrahlen ausgehen sind ... Bilder |
| Mittelpunktsstrahl | Der durch das Linsenzentrum fast unabgelenkt verlaufende Strahl |
| Brennpunkt | In diesem Punkt schneiden sich parallel zur optischen Achse verlaufende Strahlen nach der Brechung durch eine Linse auf der optischen Achse. |
| Konkavlinse | Lateinischer Begriff für Zerstreuungslinse |
.. basiert auf dem Quiz-Skript Framework
Kreuzworträtsel zu Fernrohren
Kreuzworträtsel
| Segmentspiegeln | Der Hauptspiegel vieler großer Teleskope besteht aus ... . |
| Okular | Name der augenseitigen Linse |
| Opernglas | häufiger heutiger Verwendungszweck des Galilei-Fernrohrs |
| Galilei | Wissenschaftler der das Holländische Fernrohr für astronomische Zwecke benutzte |
| Refraktor | lateinischer Begriff für Linsenfernrohr |
| Sehwinkel | Winkel der die Größe des Netzhautbildes bestimmt |
| Fangspiegel | Name des um 45° zur optischen Achse geneigten Spiegels im Newtonteleskop |
| Radioteleskop | Das Teleskop Effelsberg in der Eifel ist ein ... . |
| Cassegrain | Konstrukteur eines Spiegelteleskops mit durchbohrtem Hauptspiegel |
| Lipperhey | Erfinder des Fernrohrs |
| Hubble | Ein berühmtes Weltraumteleskop ist das ...-Weltraumteleskop. |
| Objektiv | Name der objektseitigen Linse |
| Newton | berühmter Wissenschaftler der 1668-1672 ein Spiegelteleskop entwickelte |
| Kepler | Erfinder des Fernrohrs das aus zwei Sammellinsen besteht. |
| binokular | lateinischer Begriff für "zweiäugig" |
.. basiert auf dem Quiz-Skript Framework
Multiple-Choice-Test zu Fernrohren
Mehrfach-Auswahl
Ein Feldstecher enthält außer dem Objektiv und dem Okular noch (zwei Prismen) (!zwei Spiegel) (!zwei Linsen)
Ein Galilei-Fernrohr hat eine Objektivbrennweite von 80 cm und eine Okularbrennweite von -10 cm. Die Länge beträgt: (70 cm) (!80 cm) (!90 cm)
Das Schmidt-Cassegrain-Teleskop hat einen durchbohrten (!Konvexspiegel) (Hohlspiegel) (!Fangspiegel)
Ein Galilei-Fernrohr hat eine Objektivbrennweite von 100 cm und eine Okularbrennweite von -20 cm. Die Vergrößerung beträgt: (!4) (5) (!6)
Das Newtonteleskop besteht aus einem Hohlspiegel, einem Okular und: (einem Fangspiegel) (!einem Konvexspiegel) (!einem weiteren Hohlspiegel)
Ein einzelner Spiegel eines Teleskops hat nach dem heutigen Stand der Technik einen maximalen Durchmesser von ca. (!2 m) (!6 m) (8 m)
Das Galilei-Fernrohr besteht aus: (!zwei Zerstreuungslinsen) (eine Zerstreuungslinse und eine Sammellinse) (!zwei Sammellinsen)
Ein Kepler-Fernrohr hat eine Objektivbrennweite von 100 cm und eine Okularbrennweite von 20 cm. Die Vergrößerung beträgt: (!4) (5) (!6)
Das Kepler-Fernrohr besteht aus: (zwei Sammellinsen) (!zwei Zerstreuungslinsen) (!eine Zerstreuungslinse und eine Sammellinse)
Ein Kepler-Fernrohr hat eine Objektivbrennweite von 80 cm und eine Okularbrennweite von 10 cm. Die Länge beträgt: (!80 cm) (!100 cm) (90 cm)
.. basiert auf dem Quiz-Skript Framework
