Liebe Schülerinnen und Schüler,

in diesem Lernpfad wird die kumulierte Binomialverteilung behandelt, die neben der „einfachen” Binomialverteilung in der Stochastik und auch im Abitur eine zentrale Rolle spielt.

Um die kumulierte Binomialverteilung zu verstehen, musst du vorher den Lernpfad über die Binomialverteilung gründlich durchgearbeitet haben. Folgende Fragen solltest du beantworten können (Die Antwort findest du im Reiter „Lösungen”.):

1. Was ist ein Bernoulli-Experiment?
2. Was ist eine Bernoulli-Kette?
3. Wie lautet die Bernoulli-Formel?
4. Nenne mindestens vier Eigenschaften von Binomialverteilungen!
5. Wie lautet die Formel für den Erwartungswert bei einer Binomialverteilung?
6. Wie lautet die Formel für die Varianz und die Standardabweichung bei einer Binomialverteilung?

Im Lernpfad über die „einfache” Binomialverteilung in diesem Ordner hat Robin Hood dreimal geschossen und die Wahrscheinlichkeit für mindestens zwei Treffer wurde mit der Bernoulli-Formel berechnet. Das ging relativ schnell. Stelle dir nun jetzt vor, dass Robin hätte 20-mal schießen müssen, und du musst die Wahrscheinlichkeit für mindestens 10 Treffer berechnen. Auch mithilfe der Bernoulli-Formel schreibst du dir jetzt die Finger wund. Du kannst dich beruhigen, hier gibt es eine Lösung. Bevor wir die Aufgabe lösen, ändern wir sie leicht ab: Robin muss 20-mal schießen. Die Trefferwahrscheinlichkeit bleibt p=0,7. Wie hoch ist die Wahrscheinlichkeit, dass Robin höchstens 10-mal trifft. Mit unserem bisherigen Wissen gilt:

X=Anzahl der Treffer; n=20; p=0,7; X≤10.

$\mathrm{P(X≤10)=P(X=0)+P(X=1)+...+P(X=9)+P(X=10)}$

$\mathrm{=B(20;0,7;0)+B(20;0,7;1)+...+B(20;0,7;9)+B(20;0,7;10)}$.

Das ist ganz schön viel Schreibarbeit und vor allem Rechenarbeit. Versuchen wir zunächst eine abkürzende Schreibweise. Hier hilft uns das elegante Summenzeichen:

$\mathrm{P(X≤10)=\sum\limits_{i=0}^{10}B(20;0,7;i)=\sum\limits_{i=0}^{10}{{20}\choose{i}}·0,7^{i}·(1-0,7)^{20-i}}$.

Allgemein kann man schreiben:

$\mathrm{P(X≤k)=\sum\limits_{i=0}^{k}B(n;p;i)=\sum\limits_{i=0}^{k}{{n}\choose{i}}·p^{i}·(1-p)^{n-i}}$.

Anhand der Summenschreibweise erkennen wir, dass die Binomialverteilungen von 0 bis k aufsummiert wurden. Und genau diese aufsummierte Binomialverteilung ist sowohl tabelliert als auch in den üblichen Taschenrechnern programmiert. Genau das ist für dich die Erleichterung. Selbstverständlich gibt es auch einen eleganten lateinischen Namen für die aufsummierte Binomialverteilung, die sogenannte kumulierte Binomialverteilung. Die dazugehörige Schreibweise ist F(n;p;k). Wir können also die obige Aufgabe wie folgt aufschreiben:

$\mathrm{P(X≤10)=F(20;0,7;10)}$.

Mit den handelsüblichen Casio-Taschenrechnern gehst du nun wie folgt vor:

Drücke folgende Tasten in folgender Reihenfolge:

MENU SETUP; 7:Verteilungsfunktionen, 1: kumulierte Binomialverteilung; 2: Variable.

Nun gebe die gegebenen Parameter k, n und p ein. (Beachte hier die Reihenfolge. Diese ist leider eine andere als die Reihenfolge in der Schreibweise F(n;p;k).) Der Wechsel zwischen den Parametern erfolgt durch Drücken der Gleich-Taste. Schließlich ergibt sich:

$\mathrm{P(X≤10)=F(20;0,7;10)≈0,0480=4,8\%}$.

Das Histogramm der kumulierten Binomialverteilung hat folgendes Aussehen:

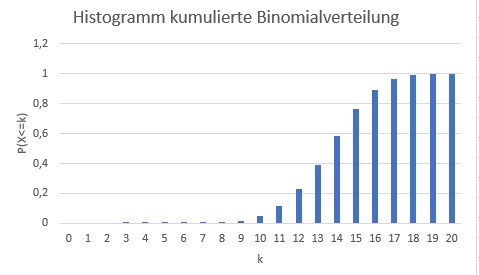
Das Histogramm sieht aus wie eine aufsteigende Treppe. Die letzte Säule hat exakt die Höhe 1. Dies musst du verstehen: Die Höhe der letzten Säule entspricht:

$\mathrm{P(X≤20)=F(20;0,7;20)=\sum\limits_{i=0}^{20}B(20;0,7;i)}$.

Und wir haben im Lernpfad über die einfache Binomialverteilung gelernt, dass alle Wahrscheinlichkeiten in der Summe 1 ergeben.

erster Fall:

Im letzten Reiter hast die Wahrscheinlichkeit für das sogenannte linksseitige Intervall gelöst (siehe den blau markierten linken Bereich im Histogramm der zugehörigen Binomialverteilung):

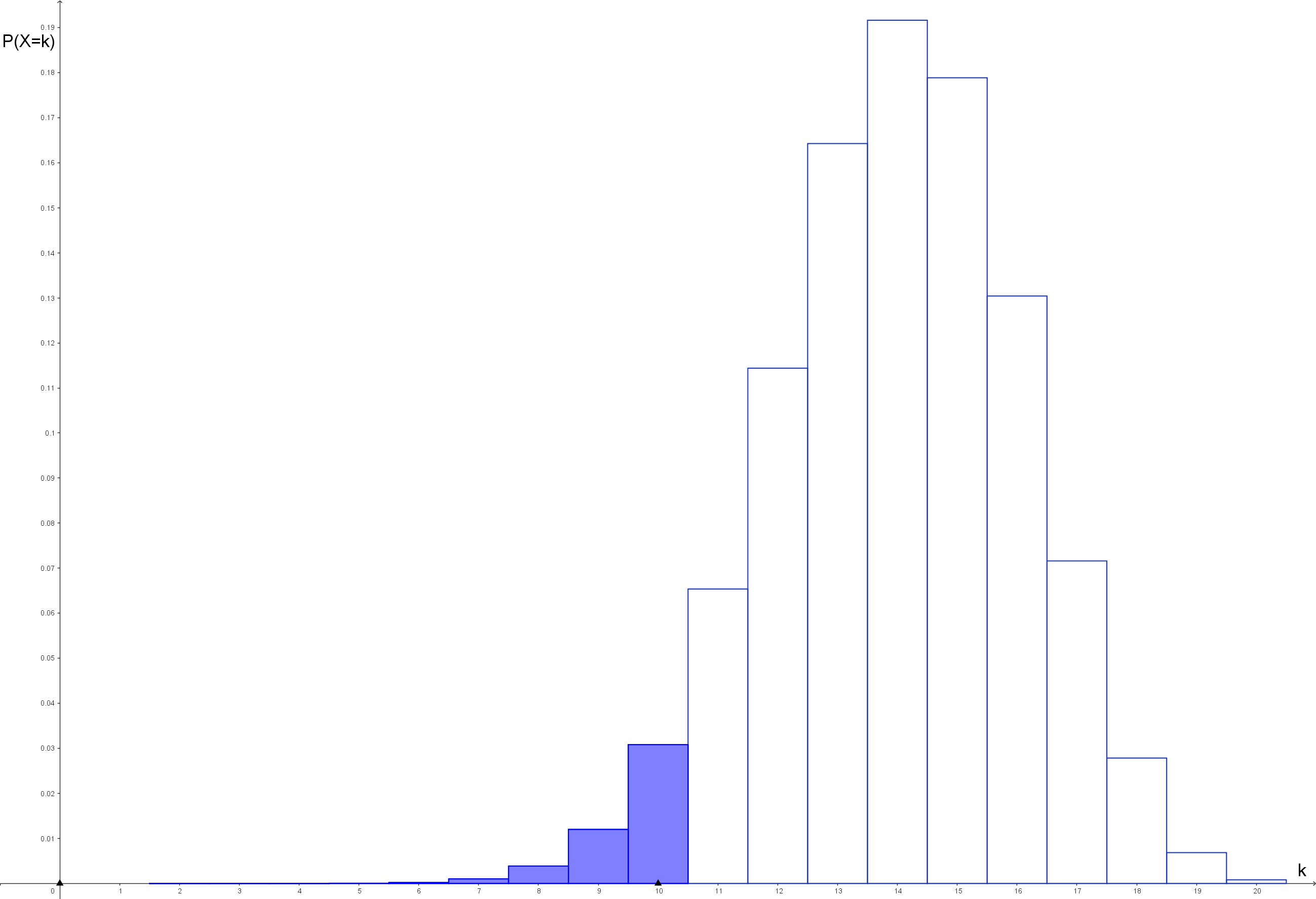
Dies ist der einfachste Standardfall, den man folgendermaßen rechnet:

$\mathrm{P(X≤10)=F(20;0,7;10)≈0,0480=4,8\%}$.

Allgemein gilt für die Wahrscheinlichkeit für ein linksseitiges Intervall:

$\underline{\mathrm{P(X≤k)=F(n;p;k)}}$.

zweiter Fall:

Du erinnerst dich, dass auch noch die Aufgabe „Wahrscheinlichkeit für mindestens 10 Treffer” zu lösen ist. Hier handelt es sich um die Wahrscheinlichkeit für ein rechtsseitiges Intervall:

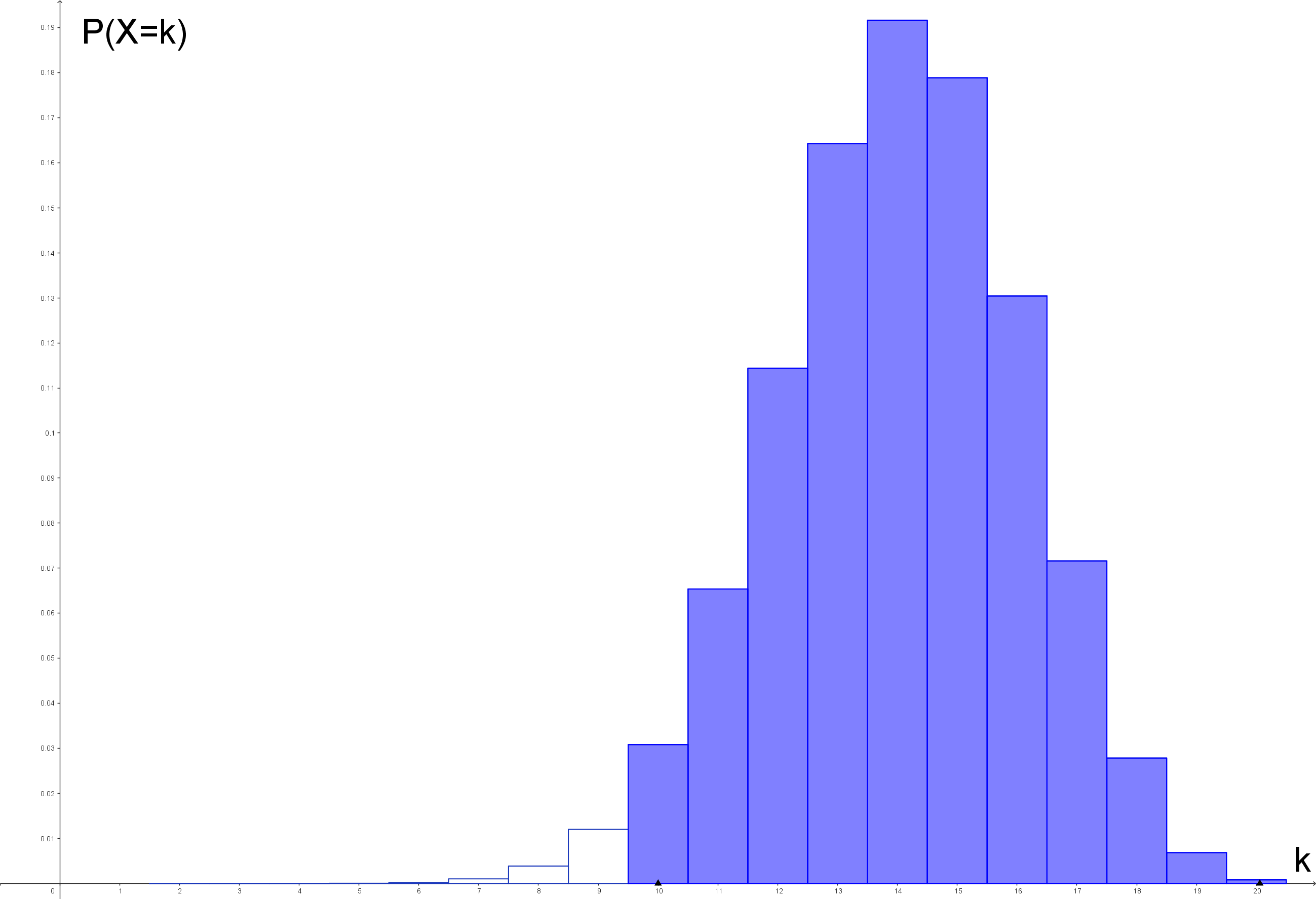
Ein genauer Blick auf das Histogramm führt zu folgender Lösung: Das Ereignis „mindestens 10 Treffer” hat als Gegenereignis „höchstens 9 Treffer”. Also gilt:

$\mathrm{P(X≥10)+P(X≤9)=1}$

$\mathrm{⇒P(X≥10)=1-P(X≤9)}$

$\mathrm{⇒P(X≥10)=1-F(20;0,7;9)}$

$\mathrm{⇒P(X≥10)≈1-0,0171=0,9829=98,29\%}$

Allgemein gilt für die Wahrscheinlichkeit für ein rechtsseitiges Intervall:

$\underline{\mathrm{P(X≥k)=1-P(X≤k-1)=1-F(n;p;k-1)}}$.

dritter Fall:

Wir können auch die Wahrscheilichkeit für 11 bis 16 Treffer berechnen. Hier handelt es sich um die Wahrscheinlichkeit für das folgende Intervall:

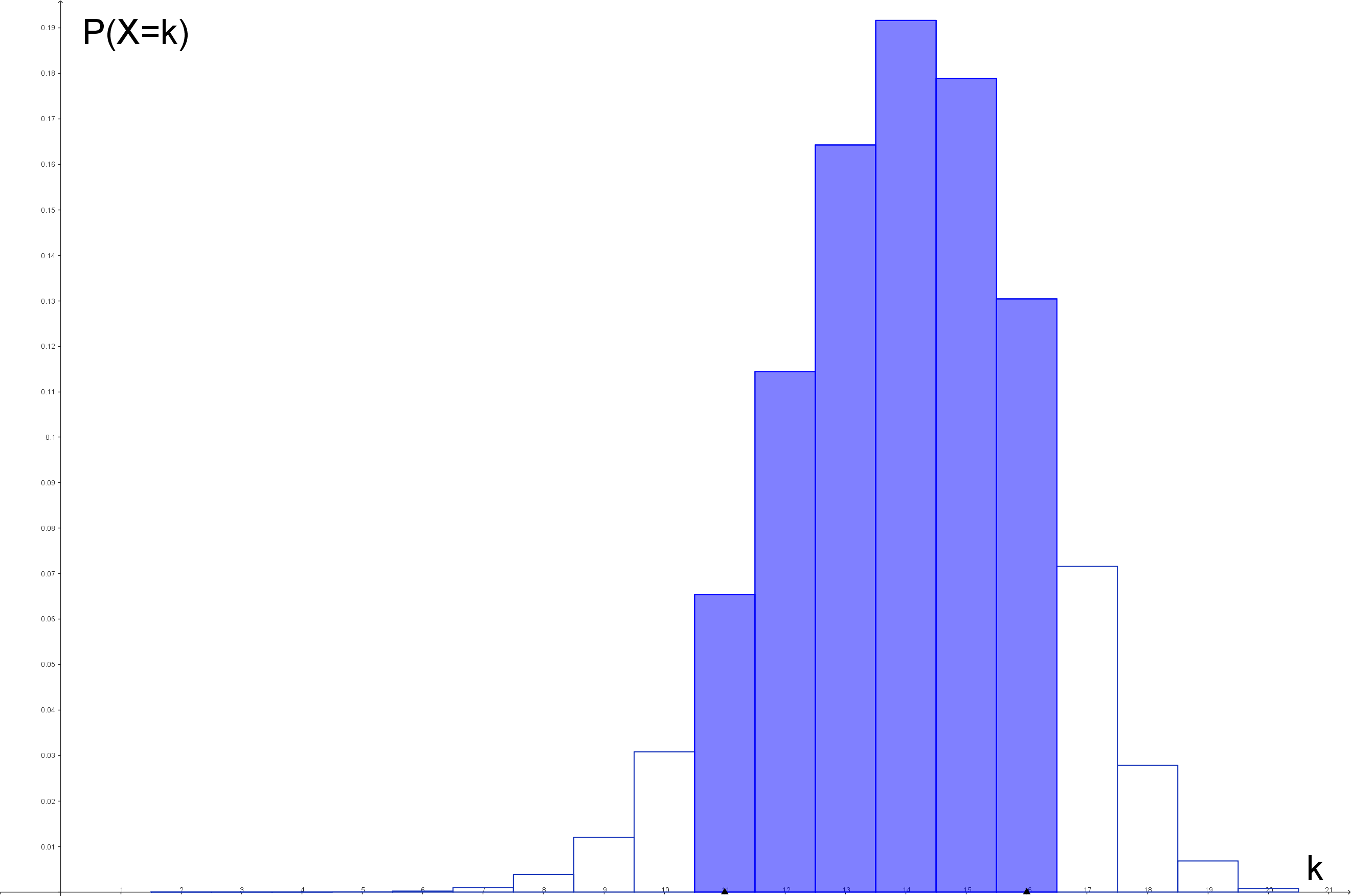
Ein genauer Blick auf das Histogramm führt auch hier zur Lösung: Wir berechnen zunächst P(X≤16). Diese ist aber um die Wahrscheinlichkeit für 0 bis 10 Treffer zu hoch. Also ziehen wir einfach P(X≤10) ab:

$\mathrm{P(11≤X≤16)=P(X≤16)-P(X≤10)}$

$\mathrm{⇒P(11≤X≤16)=F(20;0,7;16)-F(20;0,7;10)}$

$\mathrm{⇒P(11≤X≤16)≈0,8929-0,0480=0,8449=84,49\%}$

Allgemein gilt für die Intervallwahrscheinlichkeit:

$\underline{\mathrm{P(k_{1}≤X≤k_{2})=P(X≤k_{2})-P(X≤k_{1}-1)}}$

$\underline{\mathrm{P(k_{1}≤X≤k_{2})=F(n;p;k_{2})-F(n;p;k_{1}-1)}}$.

vierter Fall:

Man kann sogar mit der kumulierten Binomialverteilung die Wahrscheinlichkeit für genau k Treffer berechnen, z.B. für genau 12 Treffer. Hier handelt es sich um das folgende „Intervall”:

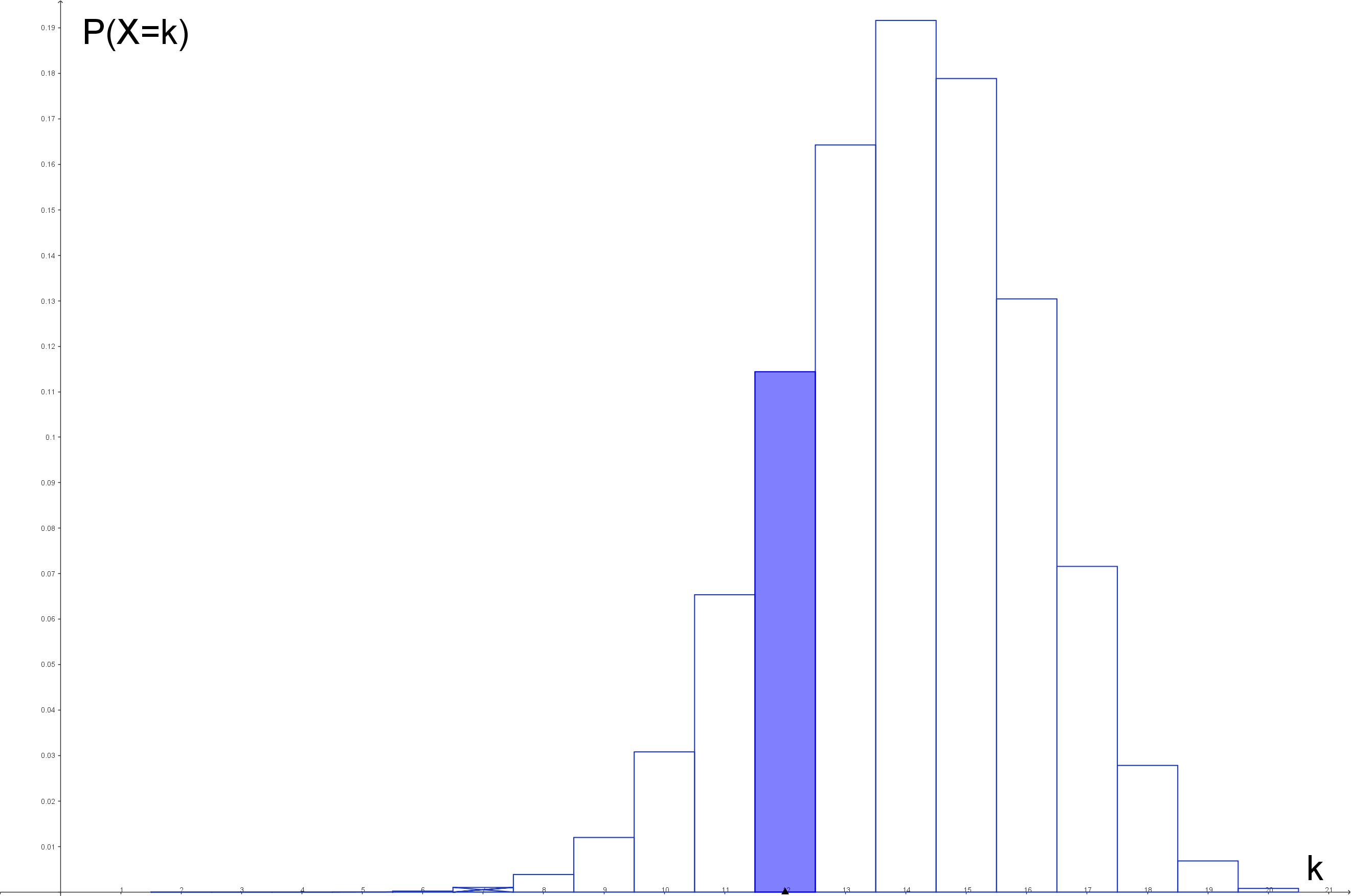
Anhand des Histogramms erkennt man, dass wir von P(X≤12) die Wahrscheinlichkeit von 0 bis 11 Treffern abziehen müssen:

$\mathrm{P(X=12)=P(X≤12)-P(X≤11)}$

$\mathrm{P(X=12)=F(20;0,7;12)-F(20;0,7;11)}$

$\mathrm{P(X=12)≈0,2277-0,1133=0,1144=11,44\%}$

Allgemein gilt für die sogenannte Punktwahrscheinlichkeit:

$\underline{\mathrm{P(X=k)=P(X≤k)-P(X≤k-1)}}$

$\underline{\mathrm{P(X=k)=F(n;p;k)-F(n;p;k-1)}}$.

Löse alle Rechenaufgaben mit der kumulierten Binomialverteilung! Die Lösungen findest du im Reiter „Lösungen”.

1.) In einer Urne befinden sich 4 schwarze und 6 weiße Kugeln. Es wird 15-mal mit Zurücklegen gezogen. X sei die Anzahl der gezogenen schwarzen Kugeln.

a) Stelle das Histogramm von B(n;p;k) mit einem geeigneten Programm dar! Erläutere das Histogramm!

b) Stelle das Histogramm von F(n;p;k) mit einem geeigneten Programm dar! Erläutere das Histogramm!

c) Wie groß ist die Wahrscheinlichkeit für genau 3 gezogene schwarze Kugeln? Kontrolliere dein Ergebnis durch eine alternative Rechnung!

d) Wie groß ist die Wahrscheinlichkeit für höchstens 3 gezogene schwarze Kugeln?

e) Wie groß ist die Wahrscheinlichkeit für mindestens 3 gezogene schwarze Kugeln?

f) Wie groß ist die Wahrscheinlichkeit für 3 bis 8 gezogene schwarze Kugeln?

g) Kann man auch auf die gleiche Weise die obigen Rechnungen durchführen, wenn man ohne Zurücklegen ziehen würde?

2.) Ein Multiple-Choice-Test enthält 30 Fragen. Zu jeder Frage exisiteren 4 Antwortmöglichkeiten, von denen jeweils genau eine richtig ist. Der Test gilt als bestanden, wenn mindestens 16 Fragen richtig beantwortet sind. Wie groß ist die Wahrscheinlichkeit, dass ein Kandidat, der auf gut Glück jeweils eine Antwort ankreuzt, den Test besteht?

3.) Ein Glücksrad enthält 6 gleich große Felder, die mit 1 bis 6 durchnummeriert sind. Das Glücksrad wird 11-mal gedreht. Wie groß ist die Wahrscheinlichkeit, das höchstens 8-mal eine gerade Zahl gedreht wird?

4.) Bei einem Betrieb, der Glühlampen produziert, sind 5% der Glühlampen defekt. Aus der laufenden Produktion werden 12 Bauteile entnommen. Gehe davon aus, dass sich durch die Entnahme die „Defektwahrscheinlichkeit” von 5% nicht wesentlich ändert. Wie groß ist die Wahrscheinlichkeit, dass 2 bis 4 der entnommenen Glühlampen defekt sind?

Jetzt soll folgende Aufgabe gelöst werden: Robin Hood schießt 50-mal mit einer Trefferwahrscheinlichkeit p=0,7. Wie wahrscheinlich ist es, dass X (=Anzahl der Treffer)

a) höchstens um σ

b) höchstens um 2σ

c) höchstens um 3σ

vom Erwartungswert abweicht?

Wir benötigen für alle Aufgaben µ und σ:

$\mathrm{µ=n·p=50·0,7=35}$; $\mathrm{σ=\sqrt{n·p·(1-p)}=\sqrt{50·0,7·0,3}≈3,24}$.

a) µ-σ=35-3,24=31,76; µ+σ=35+3,24=38,24. Im Intervall [31,76;38,24] liegen alle X-Werte von 32 bis 38. Wir müssen also P(32≤X≤38) berechnen:

P(32≤X≤38)=P(X≤38)-P(X≤31)=F(50;0,7;38)-F(50;0,7;31)

                   ≈0,8610-0,1406=0,7204=72,04%.

Die 1σ-Umgebung des Erwartungswerts ist im folgenden Histogramm der zugehörigen Binomialverteilung blau markiert:

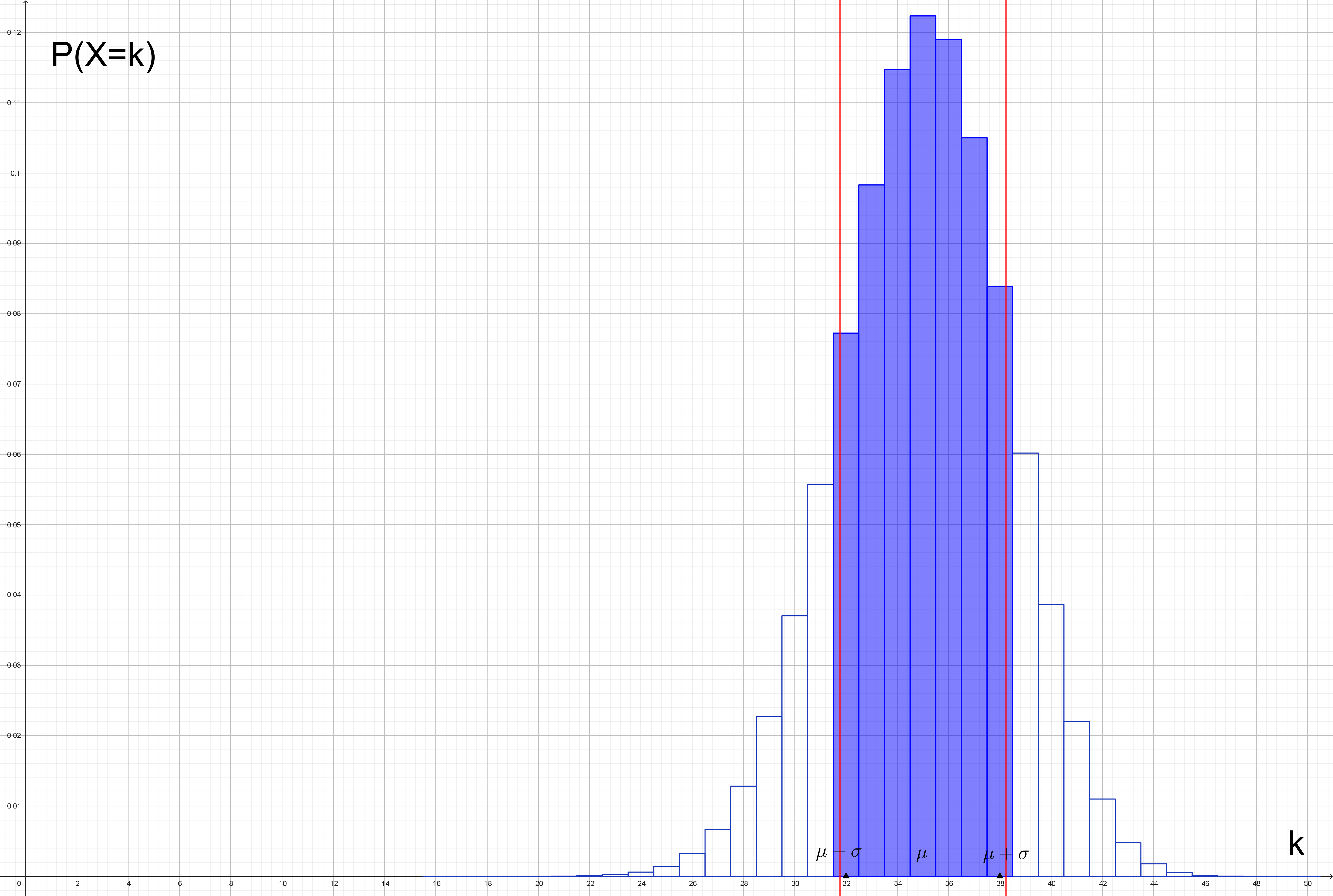
b) µ-2σ=35-2·3,24=28,52; µ+2σ=35+2·3,24=41,48.

⇒P(29≤X≤41)=P(X≤41)-P(X≤28)=F(50;0,7;41)-F(50;0,7;28)

                      ≈0,9817-0,0251=0,9566=95,66%.

c) µ-3σ=35-3·3,24=25,28; µ+3σ=35+3·3,24=44,72.

⇒P(26≤X≤44)=P(X≤44)-P(X≤25)=F(50;0,7;44)-F(50;0,7;25)

                      ≈0,9993-0,0024=0,9969=99,69%.

Wenn du weitere analoge Rechnungen durchführen würdest und darauf achten würdest, dass σ>3 ist, dann würdest du feststellen, dass die Ergebnisse für die berechneten Wahrscheinlichkeiten ähnlich sind.

Man kann also (hier ohne Beweis) festhalten:

X sei die Anzahl der Treffer in einer Bernoulli-Kette der Länge n mit Erwartungswert µ und Standardabweichung σ.

Falls die sogenannte Laplace-Bedingung σ>3 erfüllt ist, gilt:

Ca. 68% der Werte von X liegen im Intervall [µ-σ ; µ+σ].

Ca. 95,5% der Werte von X liegen im Intervall [µ-2σ ; µ+2σ].

Ca. 99,7% der Werte von X liegen im Intervall [µ-3σ ; µ+3σ].

Die Intervalle werden auch σ-Umgebungen um den Erwartungswert (1σ-Umgebung, 2σ-Umgebung, 3σ-Umgebung) genannt.

Eine typische Klausuraufgabe dazu ist z.B.:

Eine faire Münze wird 1000-mal geworfen. Gebe ein Intervall an, in dem die Anzahl der Kopfwürfe mit einer Wahrscheinlichkeit von 95,5% liegt.

Lösung:

X=Anzahl der Kopfwürfe; n=1000; p=0,5.

µ=n·p=1000·0,5=500.

$\mathrm{σ=\sqrt{n·p·(1-p)}=\sqrt{1000·0,5·(1-0,5)}≈15,81>3}$.

Die Laplace-Bedingung ist erfüllt. Also können wir die 2σ-Umgebung wegen der gegebenen Wahrscheinlichkeit von 95,5% berechnen:

µ-2σ=500-2·15,81=468,38.

µ+2σ=500+2·15,81=531,62.

Das gesuchte Intervall ist: [469;531].

Beachte: Bei der unteren Grenze des gesuchten Intervalls musst du aufrunden, bei der oberen Grenze musst du abrunden, damit du im gesuchten Intervall bleibst.

Lösungen zum Reiter Voraussetzungen:

1.) Ein Bernoulli-Experiment ist ein Zufallsexperiment mit genau zwei unterschiedlichen Ausgängen $\mathrm{E}$ und $\mathrm{\bar{E}}$.

2.) Wird ein Bernoulli-Experiment n-mal wiederholt und bleibt dabei die Trefferwahrscheinlichkeit p bei jeder Durchführung des Experiments gleich, so nennt man das eine Bernoulli-Kette der Länge n mit der Trefferwahrscheinlichkeit p.

3.) $\mathrm{P(X=k)={{n}\choose{k}}·p^{k}·(1-p)^{n-k}}$.

4.) Vier wichtige Eigenschaften:

• Je größer p ist, umso weiter rechts liegt das Maximum der Binomialverteilung.
• Für $\mathrm{p=0,5}$ ist die Binomialverteilung symmetrisch: $\mathrm{B(n;0,5;k)=B(n;0,5;n-k)}$.
• Je größer n ist, umso flacher wird die Binomialverteilung.
• Je größer n ist, umso symmetrischer wird die Binomialverteilung.

5.) $\mathrm{µ=E(X)=n·p}$.

6.) $\mathrm{V(X)=n·p·(1-p)}$ und $\mathrm{σ=\sqrt{V(X)}=\sqrt{n·p·(1-p)}}$.

Lösungen zum Reiter Aufgaben:

1.)a) Die Parameter sind: $\mathrm{n=15}$ und $\mathrm{p=\frac{4}{4+6}=\frac{4}{10}=0,4}$. Das Histogramm wurde mit Excel angefertigt:

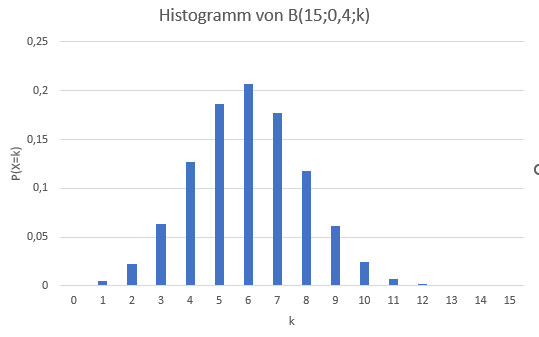
Das Histogramm hat sein Maximum bei $\mathrm{X=6}$, denn $\mathrm{E(X)=n·p=15·0,4=6}$ und die Standardabweichung ist

$\mathrm{σ=\sqrt{15·0,4·0,6}≈1,9}$.

b) Das Histogramm wurde mit Excel erstellt:

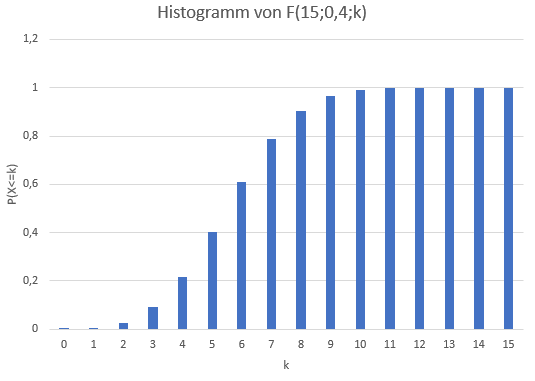
Das Histogramm sieht aus wie eine aufsteigende Treppe. Es hat sein Maximum bei $\mathrm{X=15}$, dort ist $\mathrm{F(15;0,4;15)=1}$.

c) P(X=3)=P(X≤3)-P(X≤2)=F(15;0,4;3)-F(15;0,4;2)

               ≈0,0905-0,0271=0,0634=6,34%.

Alternative Rechnung: P(X=3)=B(15;0,4;3)≈0,0633=6,33%. Dieses Ergebnis stimmt bis auf Rundungsfehler mit dem obigen Ergebnis überein.

d) P(X≤3)=F(15;0,4;3)≈0,0905=9,05%.

e) P(X≥3)=1-P(X≤2)=1-F(15;0,4;2)≈1-0,0271=0,9729=97,29%.

f) P(3≤X≤8)=P(X≤8)-P(X≤2)=F(15;0,4;8)-F(15;0,4;2)

                  ≈0,9050-0,0271=0,8779=87,79%.

g) Nein, denn die Trefferwahrscheinlichkeit p würde sich ändern. Auch 15-mal Ziehen wäre nicht möglich.

2.) X=Anzahl der richtigen Antworten; n=30; $\mathrm{p=\frac{1}{4}=0,25}$

P(X≥16)=1-P(X≤15)=1-F(30;0,25;15)≈1-0,9991=0,0009=0,09%.

3.) X=Anzahl der gedrehten geraden Zahlen, n=11; $\mathrm{p=\frac{3}{6}=0,5}$

P(X≤8)=F(11;0,5;8)≈0,9673=96,73%.

4.) X = Anzahl der entnommenen defekten Glühbirnen; n=12; p=5%=0,05

P(2≤X≤4)=P(X≤4)-P(X≤1)=F(12;0,05;4)-F(12;0,05;1)≈0,9998-0,9804=0,0194=1,94%.

Das Unterrichtsthema "Approximation der Binomialverteilung durch die Normalverteilung", das sich unmittelbar an die "kumulierte Binomialverteilung" anschließen würde, ist ein wichtiges Thema in einem Leistungskurs.

Das letzte Stochastik-Thema sowohl im Grundkurs als auch im Leistungskurs sind Hypothesentests. Hier musst du sehr viel mit der kumulierten Binomialverteilung rechnen.