Binomialverteilung
- Voraussetzungen
- Bernoulli-Ketten
- Binomialverteilung
- Anwendungen
- Eigenschaften
- Erwartungswert und Varianz
- Galton-Brett
- Vertiefung
- Lösungen I
- Lösungen II
- Ausblick
Voraussetzungen
Was musst du wissen?

Liebe Schülerinnen und Schüler,
die Binomialverteilung ist das zentrale Thema in der Stochastik und kommt in jedem Abitur vor. Auch das wichtige Testen von Hypothesen kann man ohne die Binomialverteilung nicht verstehen. In diesem Lernpfad wirst du Schritt für Schritt anhand von einfachen Beispielen und interaktiv in die Binomialverteilung eingeführt.
Die Bimomialverteilung wird erst am Ende des Kurshalbjahres Stochastik behandelt. Deshalb benötigst du viel Vorwissen. Wenn du folgende Aufgaben beantworten kannst, bist du in der Lage, die Inhalte des Lernpfads zu verstehen. Die Lösungen stehen im Reiter "Lösungen I".
- Was ist eine Wahrscheinlichkeitsverteilung?
- Wie berechnet man die Wahrscheinlichkeit des Gegenereignisses $\mathrm{P(\bar{E})}$, wenn die Wahrscheinlichkeit des Ereignisses $\mathrm{P(E)}$ gegeben ist?
- Nenne die Pfadregeln für Baumdiagramme!
- Welche Bedeutung hat der Binomialkoeffizient $\mathrm{n\choose k}$?
- Wie wird der Binomialkoeffizient $\mathrm{n\choose k}$ berechnet?
- Was ist eine Zufallsgröße und die dazugehörige Wahrscheinlichkeitsverteilung?
- Was ist der Erwartungswert?
- Wie wird der Erwartungswert berechnet?
- Was ist die Varianz und die Standardabweichung?
- Wie wird die Varianz und die Standardabweichung berechnet?
Bernoulli-Kette
Was ist eine Bernoulli-Kette?
Bevor wir mit der Binomialverteilung beginnen, musst du wissen, was eine Bernoulli-Kette ist:
Bei vielen Zufallsexperimenten interessiert man sich dafür, ob ein bestimmtes Ereignis E eintritt oder nicht. Es gibt also nur zwei Ausgänge des Experiments: $\mathrm{E}$ und $\mathrm{\bar{E}}$. Ein solches Zufallsexperiment mit genau zwei unterschiedlichen Ausgängen nennt man Bernoulli-Experiment, benannt nach dem Schweizer Mathematiker Jakob Bernoulli (1654-1705), der als einer der Begründer der Stochastik gilt.
Tritt das Ereignis E ein, so nennt man das einen Treffer oder einen Erfolg. Tritt das Ereignis nicht ein, dann spricht man von einer Niete oder einem Misserfolg. Die Grundwahrscheinlichkeit $\mathrm{p=P(E)}$ für das Eintreten des Ereignisses E wird Trefferwahrscheinlichkeit oder Erfolgswahrscheinlichkeit genannt.
Beispiele für Bernoulli-Experimente sind:
Münzwurf: $\mathrm{E}$=„Zahl”, $\mathrm{\bar{E}}$=„Kopf”, $\mathrm{p=\frac{1}{2}}$
Würfelwurf: $\mathrm{E}$=„Eins”, $\mathrm{\bar{E}}$=„keine Eins”, $\mathrm{p=\frac{1}{6}}$
Wird ein Bernoulli-Experiment n-mal wiederholt und bleibt die Trefferwahrscheinlichkeit p bei jeder Durchführung des Experiments gleich, so spricht man von einer Bernoulli-Kette der Länge n mit der Trefferwahrscheinlichkeit p.
Untersuche bei den folgenden Experimenten, ob es sich jeweils um eine Bernoulli-Kette handelt (Die Lösungen findest du im Reiter Lösungen I.):
- Eine faire Münze wird 5-mal geworfen.
- Aus einer Urne mit 6 schwarzen und 5 weißen Kugeln wird 4-mal eine Kugel ohne Zurücklegen gezogen. E=„schwarze Kugel”
- Aus einer Urne mit 1000 schwarzen Kugeln und 400 weißen Kugeln werden 5 Kugeln ohne Zurücklegen gezogen. (Man kann das auch so formulieren: Eine Stichprobe von 5 Kugeln wird entnommen.) E=„schwarze Kugel”
- Bei 8 Personen wird untersucht, welche der vier Blutgruppen jeweils vorliegt.
- Ein Schütze schießt 15-mal auf das Zentrum einer Zielscheibe.
Die Bernoulli-Formel
Darf Robin Hood Maid Marian heiraten?

Nottingham an einem schönen und windstillen Sommertag im Jahr 1223: Der Sheriff von Nottingham hat Robin Hood aus dem Sherwood Forest zum Bogenschießen eingeladen und ihm Folgendes angeboten: Robin schießt dreimal auf eine 600 Fuß (das sind ca. 183 m) entfernte Zielscheibe. Wenn er mindestens zweimal das Zentrum der Zielscheibe trifft, darf er seine Freundin Maid Marian heiraten. Wenn nicht, wird der Sheriff der Bräutigam sein. Soll Robin auf das Angebot eingehen? Du wirst ihm bei der Entscheidungsfindung helfen und dein bisheriges Wissen über die Wahrscheinlichkeitsrechnung anwenden.
Robin ist der beste Bogenschütze Englands und hat trotz der großen Entfernung von 600 Fuß eine Trefferwahrscheinlichkeit von 70%. Robin ist in seinen besten Jahren und auch beim zweiten und dritten Schuss bleibt die Trefferwahrscheinlichkeit konstant. Du erkennst, dass es sich hier um eine Bernoulli-Kette handelt. Dabei ist n=3 und p=70%=0,7.
Robin darf heiraten, wenn er mindestens zweimal das Zentrum der Zielscheibe trifft, das heißt, wenn er zweimal oder dreimal trifft. Um die Wahrscheinlichkeiten für zwei oder drei Treffer zu berechnen, zeichnen wir ein Baumdiagramm (Dabei bedeutet T=Treffer und N=Nichttreffer oder Niete):
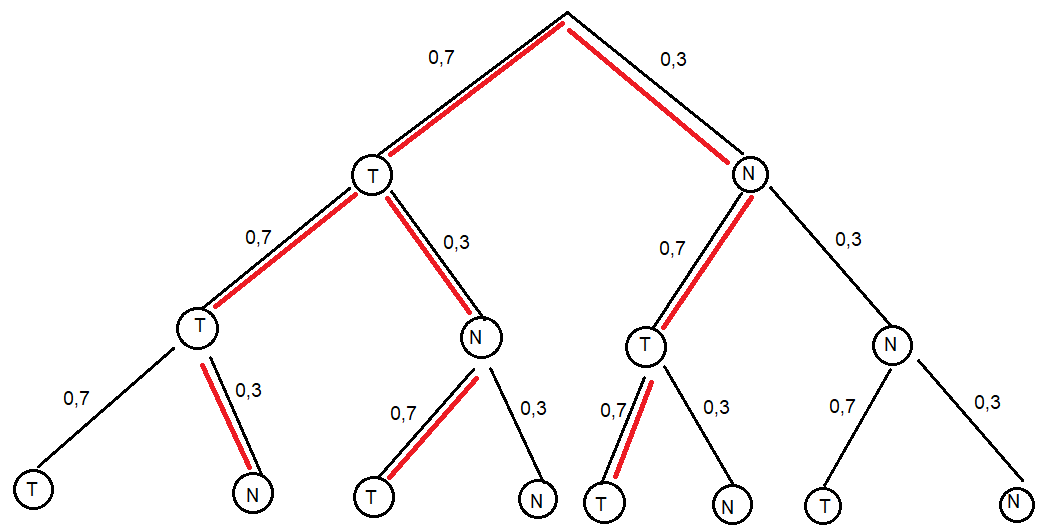
Die Wahrscheinlichkeit für drei Treffer lässt sich schnell ablesen: $\mathrm{P(„drei\,Treffer”)=0,7^{3}=0,343}$.
Jetzt berechnen wir die Wahrscheinlichkeit für zwei Treffer: Jeder Pfad mit zwei Treffern (im obigen Baumdiagramm rot markiert) hat die Pfadwahrscheinlichkeit von $\mathrm{0,7^{2}·0,3^{1}=0,147}$. Insgesamt gibt es drei Pfade mit genau zwei Treffern. Also gilt: $\mathrm{P(„zwei\,Treffer”)=3·0,147=0,441}$.
Jetzt müssen wir nur noch addieren: $\mathrm{P(„mindestens\,zwei\,Treffer”)=P(„zwei\,Treffer”)+P(„drei\,Treffer”)}$
$\mathrm{=0,441+0,343=0,784=78,4\%}$.
Du kannst also ruhigen Gewissens Robin empfehlen, auf den Vorschlag des Sheriffs einzugehen.
Stelle dir vor, dass Robin hätte 10 mal schießen müssen. Das Zeichnen eines Baumdiagrammes wäre jetzt sehr mühsam. Deshalb versuchen wir, eine Formel für die Wahrscheinlichkeit zu finden, mit der Robin genau k mal trifft. Wir bleiben bei 3 Schüssen für die folgenden Überlegungen:
Wir führen eine Zufallsvariable X ein, die die Anzahl der Treffer kennzeichnet, und wir berechnen $\mathrm{P(X=k)}$. Die Wahrscheinlichkeit für einen Pfad lässt sich leicht berechnen: Sie ist für einen Pfad der Länge $\mathrm{3}$ mit genau $\mathrm{k}$ Treffern und entsprechend $\mathrm{3-k}$ Nichttreffern: $\mathrm{0,7^{k}·0,3^{3-k}}$. Aber wie kommen wir darauf, dass es genau drei Pfade für $\mathrm{k=2}$ gibt, ohne ein Baumdiagramm benutzen zu müssen? Hier musst du dein Kombinatorik-Wissen anwenden: Es gibt nämlich genau $\mathrm{{3}\choose{2}}=3$ Kombinationen, 2 Treffer auf 3 Positionen verteilen zu können. Also gibt es $\mathrm{{3}\choose{k}}$ Pfade für $\mathrm{k}$ Treffer. Jetzt haben wir alle Zutaten für die Formel zusammengestellt: Es gilt: $\mathrm{P(X=k)={{3}\choose{k}}·0,7^{k}·0,3^{3-k}}$. Nun kannst du ganz leicht die restlichen Trefferwahrscheinlichkeiten ohne Baumdiagramm bestimmen:
Wahrscheinlichkeit für genau $\mathrm{0}$ Treffer: $\mathrm{P(X=0)={{3}\choose{0}}·0,7^{0}·0,3^{3}=1·1·0,3^{3}=0,027}$.
Wahrscheinlichkeit für genau $\mathrm{1}$ Treffer: $\mathrm{P(X=1)={{3}\choose{1}}·0,7^{1}·0,3^{2}=3·0,7·0,3^{2}=0,189}$.
Für die Berechnung des Binomialkoeffizienten $\mathrm{{{n}\choose{k}}}$ musst du nicht mit der komplizierten Formel $\mathrm{\frac{n!}{k!·(n-k)!}}$ arbeiten, sondern du kannst auf deinem Taschenrechner "nCr" benutzen (auf den meisten Taschenrechnern mittel SHIFT und der Geteilt-Taste auswählbar). Und du kannst dir merken, dass $\mathrm{{{n}\choose{0}}=1}$ und $\mathrm{{{n}\choose{n}}=1}$ ist. Das erleichtert das Rechnen sehr.
Im Folgenden stellen wir die Wahrscheinlichkeiten für alle möglichen Trefferanzahlen in Form einer Tabelle zusammen und zeichnen das dazugehörige Histogramm:
| k | $\mathrm{P(X=k)}$ |
| 0 | 0,027 |
| 1 | 0,189 |
| 2 | 0,441 |
| 3 | 0,343 |
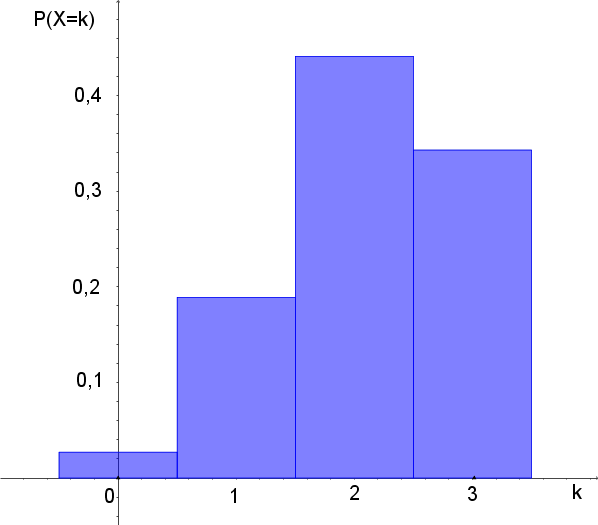
Du kannst leicht nachrechnen, dass die Summe aller Trefferanzahlwahrscheinlichkeiten $\mathrm{1}$ ist, und du siehst deutlich anhand des Histogramms, dass das Maximum der Wahrscheinlichkeit bei 2 Treffern liegt.
Da die Anzahl der Pfade für eine bestimmte Anzahl von Treffern mittels des Binomialkoeffizienten berechnet werden kann, nennt man die Trefferanzahl $\mathrm{X}$ in einer Bernoulli-Kette eine binomialverteilte Zufallsvariable.
Wir können nun die Binomialverteilung definieren:
Die Anzahl X der Treffer in einer Bernoulli-Kette der Länge n ist eine Zufallsvariable, die die Werte 0 bis n annehmen kann. Die Wahrscheinlichkeitsverteilung von X wird Binomialverteilung genannt.
Wir verallgemeinen jetzt die oben hergeleitete Formel so, dass n-mal geschossen wird, d. h., unsere Bernoulli-Kette hat jetzt die Länge n. Die Trefferwahrscheinlichkeit pro Schuss ist jetzt p und die Nietenwahrscheinlichkeit entsprechend 1-p. Dann gilt:
$\mathrm{P(X=k)={{n}\choose{k}}·p^{k}·(1-p)^{n-k}}$.
Die Formel wird die Formel von Bernoulli oder kurz Bernoulli-Formel genannt.
Die Wahrscheinlichkeit für k Treffer bei einer binomialverteilten Zufallsvariable wird auch als $\mathrm{B(n;p;k)}$ seltener auch als $\mathrm{B_{n,p}(k)}$ bezeichnet. Auf den folgenden Reitern wird immer die erste Bezeichnung verwendet.
Anwendungen
Bist du fit?
Es folgen jetzt Aufgaben, bei denen du das Gelernte einüben kannst.
Die erste Aufgabe enthält eine ausführliche Musterlösung. Die Lösungen zu den anderen Aufgaben findest du im Reiter Lösungen II.
1.) Robin schießt 5-mal. Die Trefferwahrscheinlichkeit bleibt 70%.
a) Wie hoch ist die Wahrscheinlichkeit, dass er mindestens 3-mal trifft?
b) Welche Trefferzahl ist die wahrscheinlichste?
c) Stelle die Wahrscheinlichkeitsverteilung in einem Histogramm dar!
Musterlösung:
a) Es liegt eine Bernoulli-Kette vor mit $\mathrm{X=Anzahl\,der\,Treffer}$; $\mathrm{n=5}$; $\mathrm{p=70\%=0,7}$ und $\mathrm{X\geq3}$.
$\mathrm{P(X\geq3)=P(X=3)+P(X=4)+P(X=5)}$
$\mathrm{=B(5;0,7;3)+B(5;0,7;4)+B(5;0,7;5)}$
$\mathrm{={5\choose3}·0,7^{3}·0,3^{2}+{5\choose4}·0,7^{4}·0,3^{1}+{5\choose5}·0,7^{5}·0,3^{0}}$
$\mathrm{={5\choose3}·0,7^{3}·0,3^{2}+{5\choose4}·0,7^{4}·0,3+1·0,7^{5}·1}$
$\mathrm{=0,3087+0,36015+0,16807}$
$\mathrm{=0,83692≈83,7\%}$
Für die weiteren Aufgaben darfst du auch Tabellen benutzen. Für die häufigsten Fälle gibt es Tabellen zur Binomialverteilung. Am schnellsten ist der Taschenrechner. Bei den Taschenrechnern der CASIO-Familie gehst du, wie folgt, vor:
Drücke folgende Tasten in folgender Reihenfolge:
MENU SETUP; 7: Verteilungsfunktionen, 4: Binomial-Dichte; 2: Variable.
Nun gebe die gegebenen Parameter k, n und p ein. (Beachte hier die Reihenfolge. Diese ist leider eine andere als die Reihenfolge in der Schreibweise $\mathrm{B(n;p;k)}$.) Der Wechsel zwischen den Parametern erfolgt durch Drücken der Gleich-Taste.
So ersparst du dir die langen Eingaben mit den Binomialkoeffizienten:
$\mathrm{P(X\geq3)=P(X=3)+P(X=4)+P(X=5)}$
$\mathrm{=B(5;0,7;3)+B(5;0,7;4)+B(5;0,7;5)}$
$\mathrm{=0,3087+0,36015+0,16807}$
$\mathrm{=0,83692≈83,7\%}$
Achtung: Du darfst jetzt nicht denken, dass du die Bernoulli-Formel vergessen darfst. Im taschenrechnerfreien Teil einer Klausur oder bei Interpretationsaufgaben ist der Umgang und vor allem das Verstehen der Bernoulli-Formel sehr wichtig.
b) Für die Lösung von b) musst du nur noch $\mathrm{P(X=0)}$; $\mathrm{P(X=1)}$ und $\mathrm{P(X=2)}$ ausrechnen:
$\mathrm{P(X=0)=B(5;0,7;0)=0,00243}$
$\mathrm{P(X=1)=B(5;0,7;1)=0,02835}$
$\mathrm{P(X=2)=B(5;0,7;2)=0,1323}$
(Zur Kontrolle kannst du jetzt alle Wahrscheinlichkeiten addieren. Es muss $\mathrm{1}$ herauskommen.)
Der Vergleich der Wahrscheinlichkeiten ergibt, dass die Trefferzahl $\mathrm{X=4}$ am wahrscheinlichsten ist.
c) Das manuelle Zeichnen ist recht mühsam, aber eine gute Übung. In der Regel reicht es, wenn du die Aufgabe mit einem geeigneten Programm wie z.B. GeoGebra oder Excel löst. Die folgende Lösung wurde in Excel erstellt:
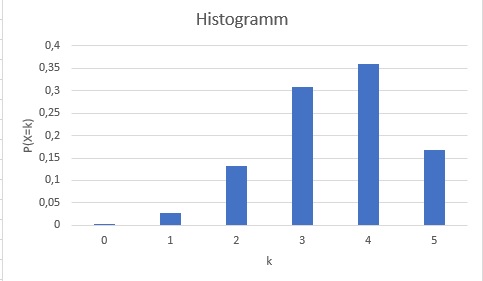
2.) In einer Urne befinden sich 4 schwarze und 6 weiße Kugeln. Berechne die Wahrscheinlichkeit, dass von 3 mit Zurücklegen gezogenen Kugeln eine schwarz und 2 weiß sind?
3.) Ein Multiple-Choice Test enthält 5 Fragen. Zu jeder Frage existieren 4 Antwortmöglichkeiten, von denen jeweils genau eine richtig ist. Der Test gilt als bestanden, wenn mindestens 3 Fragen richtig beantwortet sind. Wie groß ist die Wahrscheinlichkeit, dass ein Kandidat, der willkürlich jeweils eine Antwort ankreuzt, den Test besteht?
4.) Hans und Peter spielen Schach. Hans gewinnt im Durchschnitt 3 von 4 Partien. Wie wahrscheinlich ist, dass Hans 5 von 7 Partien gewinnt?
5.) Ein Glücksrad enthält 6 gleich große Felder, die mit 1 bis 6 durchnummeriert sind. Das Glücksrad wird 11-mal gedreht. Wie groß ist die Wahrscheinlichkeit, dass genau 8-mal eine gerade Zahl gedreht wird?
6.) Bei einem Betrieb, der Glühlampen produziert, sind 5% der Glühlampen defekt. Aus der laufenden Produktion werden 12 Bauteile übernommen.
a) Welche Annahme muss getroffen werden, damit man angenähert von einer Binomialverteilung ausgehen kann?
b) Wie groß ist die Wahrscheinlichkeit, dass genau 3 der entnommenen Bauteile defekt sind?
7.) Hans und Peter spielen Tischtennis. Peter gewinnt durchschnittlich mit einer Wahrscheinlichkeit von 80%. Es wird 10-mal gespielt. Gebe zu jedem Term ein Ereignis an, dessen Wahrscheinlichkeit berechnet wird durch:
a) $\mathrm{{10\choose6}·0,8^{6}·0,2^{4}}$
b) $\mathrm{{10\choose10}·0,8^{10}}$
c) $\mathrm{{10\choose0}·0,2^{10}}$
8.) Begründe die Bernoulli-Formel:
$\mathrm{P(X=k)=B(n;p;k)={{n}\choose{k}}·p^{k}·(1-p)^{n-k}}$
Änderung von n
Wie ändert sich das Histogramm bei Änderung von n?
In der unteren animierten Grafik ändert sich n von 1 bis 10. Die Trefferwahrscheinlichkeit ist auf p=0,4 fest eingestellt. Beobachte das Histogramm!

Du erkennst Folgendes:
- Je größer n ist, umso flacher wird das Histogramm.
- Je größer n ist, umso symmetrischer wird das Histogramm.
Diese Beobachtungen werden später im Unterricht sehr wichtig, denn sie erklären, warum man die Binomialverteilung durch die sogenannte Normalverteilung approximieren kann. Lerne die obigen Eigenschaften deshalb auswendig!
Änderung von p
Wie ändert sich das Histogramm bei Änderung von p?
In der unteren Grafik ist n auf n=10 fest eingestellt.
Beobachte, wie sich das Histogramm verändert, wenn p sich von 0 auf 1 verändert!

Du erkennst Folgendes:
Je größer p ist, umso weiter rechts liegt das Maximum.
Für p=0,5 ist die Verteilung symmetrisch: B(n;0,5;k)=B(n;0,5,n-k).
Es gibt auch die allgemeinere Symmetriebeziehung:
B(n;p;k)=B(n;1-p;n-k), z.B. B(5;0,4;1)=B(5;0,6;4).
Dieser Zusammenhang wird oft genutzt, um aus Tabellen für die Binomialverteilung richtig abzulesen. Den Beweis für diese Symmetriebeziehung findest du im Reiter Vertiefung.
Erwartungswert und Varianz
Wie berechnet man den Erwartungswert, die Varianz und die Standardabweichung?
Berechnung des Erwartungswerts:
Um den Erwartungswert einer binomialverteilten Zufallsgröße berechnen zu können, gehst du von der Definitionsformel für den Erwartungswert aus:
$\mathrm{E(X)=\sum\limits_{k=0}^{n}k·P(X=k)}$.
Wir setzen zunächst $\mathrm{n=1}$: Dann ergibt sich:
$\mathrm{E(X)=\sum\limits_{k=0}^{1}k·P(X=k)=0·P(X=0)+1·P(X=1)}$
$\mathrm{=1·P(X=1)=1·{1\choose1}·p^{1}·(1-p)^{1-1}=1·p}$.
Nun setzen wir $\mathrm{n=2}$:
$\mathrm{E(X)=\sum\limits_{k=0}^{2}k·P(X=k)=0·P(X=0)+1·P(X=1)+2·P(X=2)}$
$\mathrm{=1·P(X=1)+2·P(X=2)=1·{2\choose1}·p^{1}·(1-p)^{2-1}+2·{2\choose2}·p^{2}·(1-p)^{2-2}}$
$\mathrm{=1·2·p·(1-p)^{1}+2·1·p^{2}·1}$
$\mathrm{=2·p·(1-p)+2·p^{2}=2p-2p^{2}+2p^{2}=2p}$
Wir vermuten $\mathrm{E(X)=n·p}$. Der Beweis für allgemeines n ist wesentlich länger als die obigen Rechnungen, aber sehr spannend. Diesen Beweis findest du im Reiter "Vertiefung". Das Ergebnis bestätigt unsere Vermutung. Im Folgenden bezeichnen wir den Erwartungswert auch mit dem griechischen Buchstaben $\mathrm{\mu}$. Wir halten fest:
Der Erwartungswert einer binomialverteilten Zufallsgröße mit den Parametern $\mathrm{\textbf{n}}$ und $\mathrm{\textbf{p}}$ ist µ$\mathrm{\textbf{=E(X)=n·p}}$.
Berechnung der Varianz und der Standardabweichung:
Wie bei der Berechnung des Erwartungswerts gehen wir von der Definitionsformel für die Varianz aus:
$\mathrm{E(X)=\sum\limits_{k=0}^{n}(k-\mu)^{2}·P(X=k)}$.
Nach sehr langen Umformungen ergibt sich für die Varianz einer binomialverteilten Zufallsgröße mit den Parametern $\mathrm{n}$ und $\mathrm{p}$:
$\mathrm{\textbf{V(X)=n·p·(1-p)}}$.
Für die Standardabweichung $\mathrm{σ=\sqrt{V(X)}}$ ergibt sich entsprechend:
$\mathrm{\textbf{σ=}\sqrt{\textbf{V(X)}}\textbf{=}\sqrt{\textbf{n·p·(1-p)}}}$.
Aufgaben zu Erwartungswert, Varianz und Standardabweichung (Die Lösungen stehen im Reiter "Lösungen II"):
1.) Berechne den Erwartungswert, die Varianz und die Standardabweichung der binomialverteilten Zufallsgröße X mit den Parametern n=3 und p=0,7.
2.) Von der binomialverteilten Zufallsgröße X ist der Erwartungswert µ=10 und die Standardabweichung σ=3 gegeben. Berechne die Parameter n und p von X.
Galton-Brett
Gibt es ein Experiment zur Binomialverteilung?
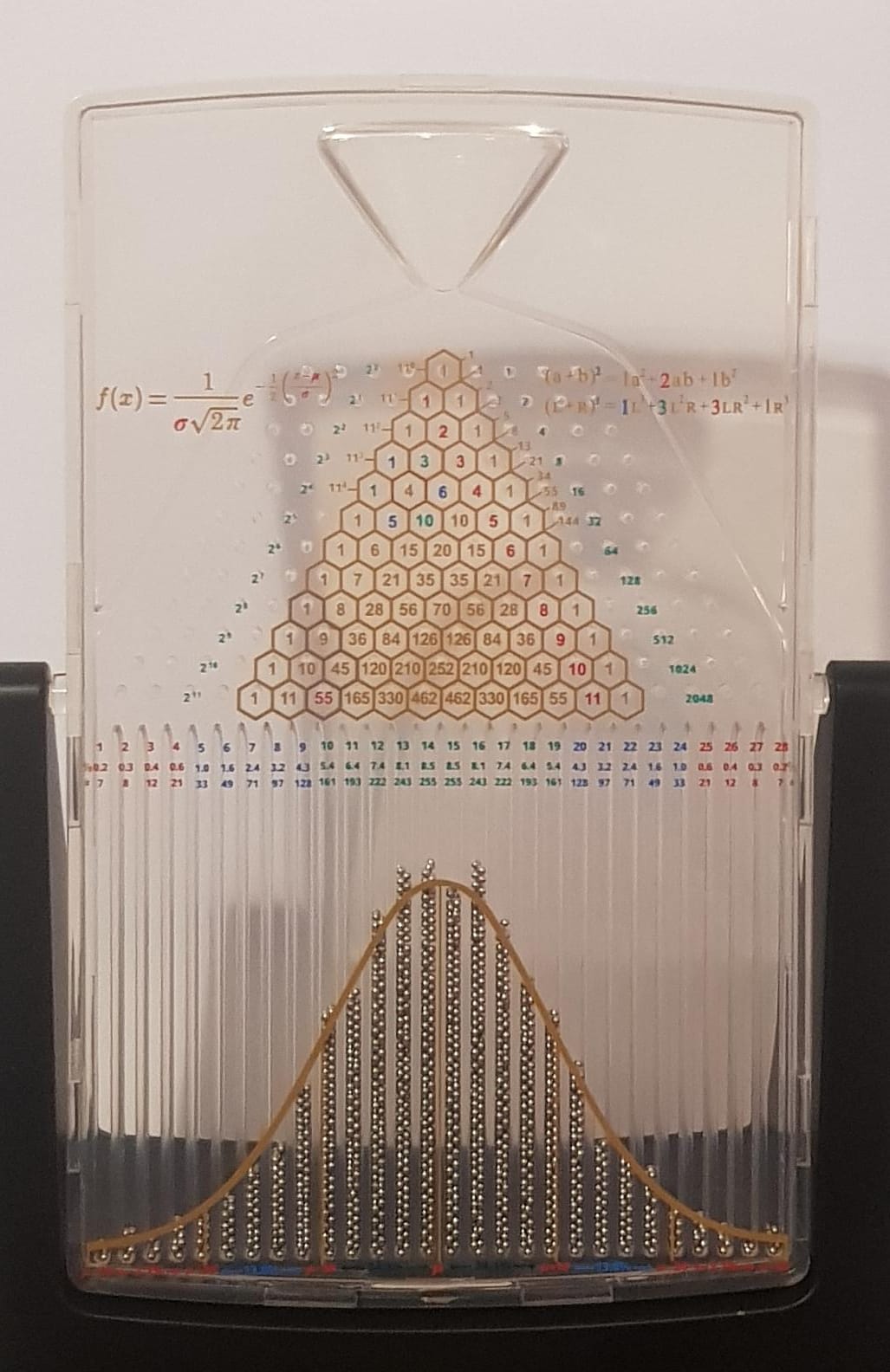
Das oben abgebildete Galton-Brett, benannt nach Sir Francis Galton (1822-1911), veranschaulicht experimentell die Binomialverteilung. (Es hat auch eine große Bedeutung in der Physik.)
Das Galton-Brett besteht aus einer regelmäßigen Anordnung von Hindernissen, an denen eine von oben eingeworfene Kugel jeweils nach links oder nach rechts abprallen kann. Nach dem Passieren der Hindernisse werden die Kugeln in Fächern aufgefangen.
Jedes Aufprallen einer Kugel auf eines der Hindernisse ist ein Bernoulli-Experiment. Das Ereignis "Kugel fällt nach rechts" kann als Treffer interpretiert werden mit der Trefferwahrscheinlichkeit p=0,5 bei symmetrischem Aufbau. Die Zahl der waagerechten Reihen von Hindernissen entspricht der Länge n der Bernoulli-Kette. Die Fachnummer, wobei die Fächer von links nach rechts und beginnend mit der Nummer 0 durchnummeriert werden, kann als die Trefferzahl X=k interpretiert werden.
Bei vielen herunterfallenden Kugeln entsteht so "experimentell" ein Histogramm der Binomialverteilung mit n=Anzahl der waagerechten Hindernisreihen und p=0,5.
Wenn du das Galton-Brett schief stellst, erhältst du das Histogramm einer Binomialverteilung mit p>0,5, wie im unteren Bild dargestellt.

Video zur Bedienung des Galton-Bretts
Vertiefung
Kannst du das beweisen?
Zunächst beweisen wir eine wichtige Eigenschaft der Binomialverteilung aus dem Reiter "Eigenschaften" :
$\mathrm{B(n;p;k)=B(n;1-p;n-k)}$:
Wir gehen von der rechten Seite aus:
$\mathrm{B(n;1-p;n-k)={{n}\choose{n-k}}·(1-p)^{n-k}·(1-(1-p))^{n-(n-k)}}$
$\mathrm{=\frac{n!}{(n-k)!·(n-(n-k))!}·(1-p)^{n-k}·(1-1+p)^{n-n+k}}$
$\mathrm{=\frac{n!}{(n-k)!·(n-n+k)!}·(1-p)^{n-k}·p^{k}}$
$\mathrm{=\frac{n!}{(n-k)!·k!}·(1-p)^{n-k}·p^{k}}$
$\mathrm{=\frac{n!}{k!·(n-k)!}·p^{k}·(1-p)^{n-k}}$
$\mathrm{={{n}\choose{k}}·p^{k}·(1-p)^{n-k}}$
$\mathrm{=B(n;p;k)}$. Damit haben wir die linke Seite erreicht, und wir sind fertig.
Nun zeigen wir für ein allgemeines n, dass für eine binomialverteilte Zufallsgröße X mit den Parametern n und p gilt (siehe Reiter "Erwartungswert und Varianz"):
$\mathrm{E(X)=n·p}$:
Wir gehen von der Definitionsformel für den Erwartungswert aus:
$\mathrm{E(X)=\sum\limits_{k=0}^{n}k·P(X=k)}$
$\mathrm{=\sum\limits_{k=0}^{n}k·{{n}\choose{k}}·p^{k}·(1-p)^{n-k}}$
Wir können den ersten Summanden mit k=0 weglassen, da 0 mal etwas immer 0 ergibt. Also folgt:
$\mathrm{=\sum\limits_{k=1}^{n}k·{{n}\choose{k}}·p^{k}·(1-p)^{n-k}}$
$\mathrm{=\sum\limits_{k=1}^{n}k·\frac{n!}{k!·(n-k)!}·p^{k}·(1-p)^{n-k}}$
$\mathrm{=\sum\limits_{k=1}^{n}k·\frac{n!}{k·(k-1)!·(n-k)!}·p^{k}·(1-p)^{n-k}}$
$\mathrm{=\sum\limits_{k=1}^{n}\frac{n!}{(k-1)!·(n-k)!}·p^{k}·(1-p)^{n-k}}$
Da wir schon vermuten, dass n·p herauskommt, versuchen wir so umzuformen, dass n und p vor dem Summenzeichen stehen:
$\mathrm{=\sum\limits_{k=1}^{n}\frac{n·(n-1)!}{(k-1)!·(n-k)!}·p^{1}·p^{k-1}·(1-p)^{n-k}}$
$\mathrm{=n·p·\sum\limits_{k=1}^{n}\frac{(n-1)!}{(k-1)!·(n-k)!}·p^{k-1}·(1-p)^{n-k}}$
Wir führen jetzt eine neue Variable $\mathrm{j=k-1}$ ein und erhalten:
$\mathrm{=n·p·\sum\limits_{j=0}^{n-1}\frac{(n-1)!}{j!·(n-1-j)!}·p^{j}·(1-p)^{n-1-j}}$
Wir führen eine weitere neue Variable $\mathrm{m=n-1}$ ein und erhalten:
$\mathrm{=n·p·\sum\limits_{j=0}^{m}\frac{m!}{j!·(m-j)!}·p^{j}·(1-p)^{m-j}}$
$\mathrm{=n·p·\sum\limits_{j=0}^{m}{{m}\choose{j}}·p^{j}·(1-p)^{m-j}}$
Die Summe aller Wahrscheinlichkeiten einer Wahrscheinlichkeitsverteilung ist 1. Also folgt schließlich:
$\mathrm{=n·p·1=n·p}$.
Lösungen I
Hast du richtig gelöst?
Deine Lösungen müssen nicht "wortgenau" mit den unteren Musterlösungen übereinstimmen. Wichtig ist, dass du "sinngemäß" richtig geantwortet hast.
Lösungen zum Reiter Voraussetzungen
1.) Gegeben sei ein Zufallsexperiment mit dem Ergebnisraum $\mathrm{Ω=\{e_{1},...,e_{m}\}}$.
Eine Zuordnung P, die jedem Elementarereignis $\mathrm{\{e_{i}\}}$ genau eine reelle Zahl $\mathrm{P(e_{i})}$ zuordnet, heißt Wahrscheinlichkeitsverteilung, wenn die beiden folgenden Bedingungen erfüllt sind:
- $\mathrm{P(e_{i})\geq0}$ für $\mathrm{1\leq{i}\leq{m}}$
- $\mathrm{P(e_{1})+...+P(e_{m})=1}$
Die Zahl $\mathrm{P(e_{i})}$ heißt dann Wahrscheinlichkeit des Elementarereignisses $\mathrm{\{e_{i}\}}$. (P von lat. probabilitas: dt. Wahrscheinlichkeit.)
2.) Die Summe der Wahrscheinlichkeit eines Ereignisses $\mathrm{E}$ und der des Gegenereignisses $\mathrm{\bar{E}}$ ist gleich $\mathrm{1}$. Daraus folgt: $\mathrm{P(\bar{E})=1-P(E)}$.
3.) Pfadregeln für Baumdiagramme:
Mehrstufige Zufallsexperimente können durch Baumdiagramme dargestellt werden. Dabei stellt jeder Pfad ein Ergebnis des Zufallsexperimentes dar.
- Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt aller Zweigwahrscheinlichkeiten längs des zugehörigen Pfades (Pfadwahrscheinlichkeit).
- Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der zugehörigen Pfadwahrscheinlichkeiten.
4.) Es gibt $\mathrm{{n\choose k}}$ Möglichkeiten, aus einer Urne mit n unterscheidbaren Kugeln eine Teilmenge von k Kugeln zu entnehmen. Oder: Eine n-elementige Menge hat genau $\mathrm{{n\choose k}}$ k-elementige Teilmengen.
5.) $\mathrm{{n\choose k} = \frac{n!}{k!·(n-k)!}}$ mit $\mathrm{n!=n·(n-1)·...·2·1}$ bzw. $\mathrm{k!=k·(k-1)·...·2·1}$.
6.) Eine Zuordnung $\mathrm{X}$$\mathrm{:Ω→\mathbb{R}}$, die jedem Ergebnis eines Zufallsversuchs eine reelle Zahl zuordnet, heißt Zufallsgröße oder Zufallsvariable.
Mit $\mathrm{X=x_{i}}$ wird das Ergebnis bezeichnet, zu dem alle Ergebnisse des Zufallsversuchs gehören, deren Eintritt dazu führt, dass die Zufallsgröße $\mathrm{X}$ den Wert $\mathrm{x_{i}}$ annimmt.
Ordnet man jedem möglichen Wert $\mathrm{x_{i}}$, den die Zufallsgröße $\mathrm{X}$ annehmen kann, die Wahrscheinlicchkeit $\mathrm{P(X=x_{i})}$ zu, mit der sie diesen Wert annimmt, so erhält man die Wahrscheinlichkeitsverteilung der Zufallsgröße $\mathrm{X}$.
7.) Der Erwartungswert von $\mathrm{X}$ ist das gewichtete arithmetische Mittel der Elemente der Wertemenge von $\mathrm{X}$. (Als Gewichte dienen die den Elementen $\mathrm{x_{i}}$ der Wertemenge zugeordneten Wahrscheinlichkeiten $\mathrm{P(X=x_{i})}$.)
8.) Der Erwartungswert wird mit folgender Formel berechnet: $\mathrm{μ=E(X)=\sum\limits_{i}x_{i}·P(X=x_{i})}$.
9.) Das Streuungsmaß der Zufallsgröße $\mathrm{X}$, das durch die Summe der quadratischen Abweichungen der Werte $\mathrm{x_{i}}$ vom Erwartungswert gebildet wird, ist die Varianz.
Das Streuungsmaß, das durch die Wurzel der Varianz gebildet wird, ist die Standardabweichung.
10.) Die Varianz wird mit folgender Formel berechnet: $\mathrm{V(X)=\sum\limits_{i}(x_{i}-µ)^{2}·P(X=x_{i})}$.
Für die Standardabweichung gilt: $\mathrm{σ(X)=\sqrt{V(X)}}$.
Lösungen zum Reiter "Bernoulli-Ketten"
1.) Ja, das ist eine Bernoulli-Kette mit z. B. E="Kopf" und $\mathrm{p=\frac{1}{2}}$ und n=5
2.) Nein, das ist keine Bernoulli-Kette: Es werden zwar nacheinander 4 Bernoulli-Experimente durchgefüht, aber die Trefferwahrscheinlichkeit ist nicht konstant, da ohne Zurücklegen gezogen wird.
3.) Wenn du dich für nein entschieden ist, ist das erstmal richtig, denn auch hier wird ohne Zurücklegen gezogen. Aber die Trefferwahrscheinlichkeit p bleibt fast konstant, weil in der Urne sehr viele schwarze und weiße Urnen liegen und nur wenige Kugeln gezogen werden. Man kann also approximativ von einer Bernoulli-Kette mit n=5 und $\mathrm{p≈\frac{1000}{1400}=\frac{5}{7}}$ ausgehen.
4.) Nein, das ist keine Bernoulli-Kette: Es gibt hier mehr als zwei Ausgänge.
5.) Unter der Vorauusetzung, dass der Schütze nicht müde wird, also die Trefferwahrscheinlichkeit p konstant bleibt, kann man von einer Bernoulli-Kette mit n=15 ausgehen.
Lösungen II
Hast du richtig gerechnet?
Lösungen zu den Aufgaben im Reiter "Anwendungen":
2.) $\mathrm{X=Anzahl\,der\,schwarzen\,Kugeln}$
$\mathrm{n=3}$
$\mathrm{p=\frac{4}{4+6}=\frac{4}{10}=0,4}$
$\mathrm{X=1}$
$\mathrm{P(X=1)=B(3;0,4;1)=0,432=43,2\%}$
3.) $\mathrm{X=Anzahl\,der\,richtig\,beantworteten\,Fragen}$
$\mathrm{n=5}$
$\mathrm{p=\frac{1}{4}=0,25}$
$\mathrm{X\geq3}$
$\mathrm{P(X\geq3)=P(X=3)+P(X=4)+P(X=5)}$
$\mathrm{=B(5;0,25;3)+B(5;0,25;4)+B(5;0,25;5)}$
$\mathrm{≈0,0879+0,0146+0,0010=0,1035=10,35\%}$
4.) $\mathrm{X=Anzahl\,der\,von\,Hans\,gewonnenen\,Partien}$
$\mathrm{n=7}$
$\mathrm{p=\frac{3}{4}=0,75}$
$\mathrm{X=5}$
$\mathrm{P(X=5)=B(7;0,75;5)=0,3115=31,15\%}$
5.) $\mathrm{X=Anzahl\,der\,gedrehten\,geraden\,Zahlen}$
$\mathrm{n=11}$
$\mathrm{p=\frac{3}{6}=0,5}$
$\mathrm{X=8}$
$\mathrm{P(X=8)=B(11;0,5;8)=0,0806=8,06\%}$
6.)a) $\mathrm{Man\,muss\,annehmen,\,dass\,sehr\,viele\,Glühlampen\,produziert\,werden.}$
$\mathrm{Die\,Entnahme\, von\,12\,Bauteilen\,(Ziehen\,ohne\,Zurücklegen)}$
$\mathrm{ändert\,dann\,nur\,wenig\,die \,Ausschusswahrscheinlichkeit\,von\,5\%.}$
b) $\mathrm{X=Anzahl\,der\,entnommenen\,defekten\,Glühlampen}$
$\mathrm{n=12}$
$\mathrm{p=5\%=0,05}$
$\mathrm{X=3}$
$\mathrm{P(X=3)=B(12;0,05;3)=0,0173=1,73\%}$
7.) Aus der Aufgabenstellung ergibt sich $\mathrm{n=10}$, $\mathrm{p=0,8}$ und
$\mathrm{X=Anzahl\,der\,Gewinne\,von\,Peter}$
a) Das ist die Wahrscheinlichkeit, dass Peter 6-mal gewinnt.
b) Das ist die Wahrscheinlichkeit, dass Peter genau 10-mal gewinnt. Hier musst du dir $\mathrm{·0,2^{0}}$ zur Formel dazudenken.
c) Das ist die Wahrscheinlichkeit, dass Peter genau 0-mal gewinnt, also 10-mal verliert. Hier musst du dir $\mathrm{·0,8^{0}}$ zur Formel dazudenken.
8.) Man betrachte alle Pfade der Länge $\mathrm{n}$ mit $\mathrm{k}$ Treffern und entsprechend $\mathrm{n-k}$ Nieten.
- Jeder dieser Pfade hat die Wahrscheinlichkeit $\mathrm{p^{k}·(1-p)^{n-k}}$.
- Es gibt $\mathrm{{{n}\choose{k}}}$ solcher Pfade.
Lösungen zu den Aufgaben im Reiter "Erwartungswert und Varianz":
1.) $\mathrm{\mu=n·p=3·0,7=2,1}$
$\mathrm{V(X)=n·p·(1-p)=3·0,7·0,3=0,63}$
$\mathrm{\sigma=\sqrt{V(X)}=\sqrt{n·p·(1-p)}=\sqrt{3·0,7·0,3}≈0,79}$
2.) $\mathrm{\sigma=\sqrt{n·p·(1-p)}⇒\sigma=\sqrt{\mu·(1-p)}⇒}$
$\mathrm{3=\sqrt{10·(1-p)}⇒9=10·(1-p)⇒0,9=1-p⇒}$
$\mathrm{-0,1=-p⇒p=0,1⇒}$
$\mathrm{10=n·0,1⇒n=100}$
Die gesuchten Parameter sind also $\mathrm{n=100}$ und $\mathrm{p=0,1}$.
Ausblick
Wie geht es weiter?
Du hast mit dem Durcharbeiten der vorherigen Reiter viel gelernt und bist in der Lage, viele Aufgaben bezüglich der Binomialverteilung zu lösen.
Du hast allerdings schon bemerkt, dass bei den "mindestens"-Aufgaben immer noch viel Schreib- und Rechenaufwand notwendig sind. Das gilt auch für "höchstens"-Aufgaben. Hier gibt es Abhilfe: die sogenannte kumulierte Binomialverteilung F(n;p;k). Was das bedeutet und wie man damit rechnet, ist Thema des Lernpfades über die kumulierte Binomialverteilung in diesem Ordner. Im Lernpfad über die kumulierte Binomialverteilung werden auch die wichtigen σ-Umgebungen des Erwartungswertes erklärt.
Die auch hier nicht behandelte Approximation der Binomialverteilung durch die Normalverteilung ist ein wichtiges Thema in einem Leistungskurs.
Das letzte Stochastik-Thema sowohl im Grundkurs als auch im Leistungskurs sind Hypothesentests. Hier musst du sehr viel sowohl mit der Binomialverteilung als auch mit der kumulierten Binomialverteilung rechnen.
