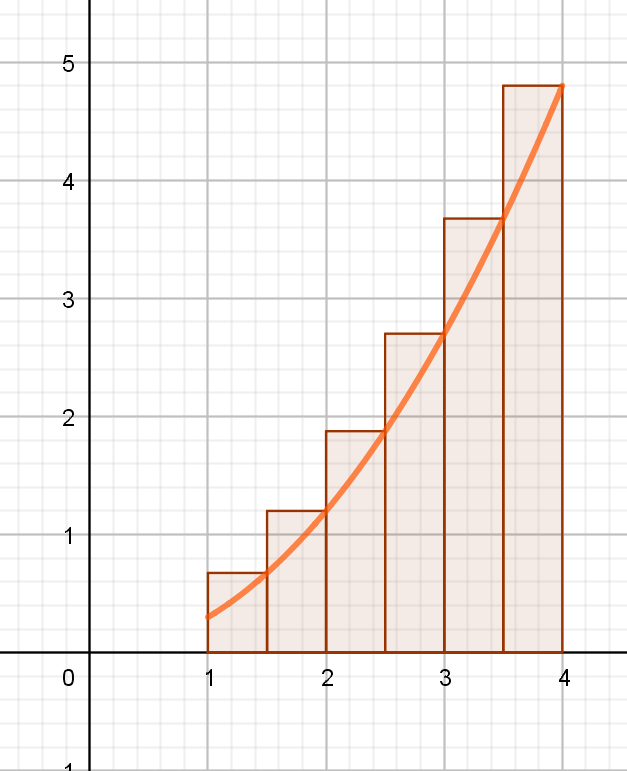
Bei krummlinig begrenzten Flächen schlug Archimedes eine Streifenmethode vor, wobei die krummlinige Begrenzung durch den Graphen x → f(x) gegeben sein soll. Diese Streifenmethode wird die Grundlage unserer ersten Berechnungen sein. Die Fläche wird durch eine Folge "einbeschriebener" und "umbeschriebener" Rechtecke angenähert. Durch fortgesetzte Unterteilung nähern sich die innere und die äußere Rechtecksumme dem gesuchten Flächeninhalt an.

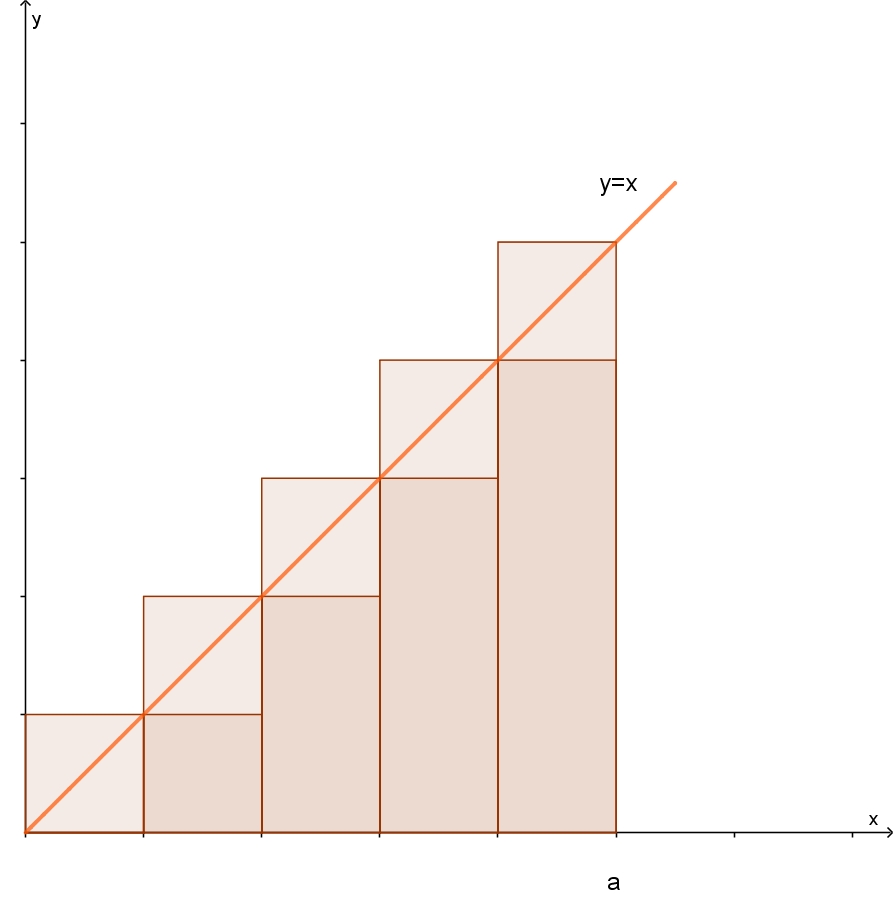
Die Gerade y=x schließt mit der x-Achse und der Geraden x=a (a>0) eine Fläche ein.

Dieser Flächeninhalt $A_{0}^{a}$ lässt sich elementar berechnen. Es gilt:

$A_{0}^{a}=\frac{1}{2}⋅a⋅a=\frac{1}{2}a^{2}$ (Dreiecksfläche = Grundseite mal Höhe durch 2)

Zur Verwendung der Streifenmethode wird das Intervall I=[0;a] in n gleich lange, abgeschlossene Teilintervalle zerlegt. Über diesen Strecken mit der Länge h=Δx=a/n werden ein- und umbeschriebene Rechtecke errichtet (siehe Reiter Einführung).

Es entsteht eine untere Treppenfläche (Untersumme s_n) und eine obere Treppenfläche (Obersumme S_n).

Bestimmung der Summen der Rechteckflächen:

Breite der Rechtecke: h

Höhe der Rechtecke: n⋅h

In der obigen Zeichnung sind fünf Teilintervalle gezeichnet:

Berechnung von S₅ und s₅:

S₅ = h⋅h + h⋅2h + h⋅3h + h⋅4h + h⋅5h = h²⋅(1+2+3+4+5)

s₅ = h⋅h + h⋅2h + h⋅3h + h⋅4h = h²⋅(1+2+3+4)

Verallgemeinerung auf n Teilintervalle (n∈$\mathbb{N}$):

S_n = h⋅h + h⋅2h + h⋅3h + h⋅4h + h⋅nh = h²⋅(1+2+...+n)

s₅ = h⋅h + h⋅2h + h⋅3h + h⋅4h + h⋅(n-1)h = h²⋅[1+2+...+(n-1)]

Sowohl bei S_n als auch bei s_n tritt eine Summe aufeinanderfolgender natürlicher Zahlen auf.

< S_n > und < s_n > stellen Zahlenfolgen dar.

Wie erhält man die Summe der ersten n natürlichen Zahlen?

Dazu benutzt man die Formel: $1+2+...+n=\sum\limits_{ν=1}^{n}ν=\frac{n(n+1)}{2}$

Für die Summen der Rechteckflächen erhält man damit:

$S_{n}=h^{2}⋅\frac{n⋅(n+1)}{2}=\frac{a^{2}}{n^{2}}⋅\frac{n^{2}(1+\frac{1}{n})}{2}=a^{2}⋅\frac{(1+\frac{1}{n})}{2}$ (Bei (n+1) wird n ausgeklammert , anschließend wird mit n² gekürzt.)

$s_{n}=h^{2}⋅\frac{(n-1)⋅n}{2}=\frac{a^{2}}{n^{2}}⋅\frac{n^{2}(1-\frac{1}{n})}{2}=a^{2}⋅\frac{(1-\frac{1}{n})}{2}$ (Denke auch hier an das Ausklammern und an das Kürzen.)

Nach den Grenzwertsätzen für Zahlenfolgen gilt:

$\lim\limits_{n→∞}a^{2}⋅\frac{(1+\frac{1}{n})}{2}=\frac{a^{2}}{2}\lim\limits_{n→∞}(1+\frac{1}{n})=\frac{a^{2}}{2}⋅1=\frac{a^{2}}{2}$ ($\frac{1}{n}$ ist eine Nullfolge)

$\lim\limits_{n→∞}a^{2}⋅\frac{(1-\frac{1}{n})}{2}=\frac{a^{2}}{2}\lim\limits_{n→∞}(1-\frac{1}{n})=\frac{a^{2}}{2}⋅1=\frac{a^{2}}{2}$

Es folgt also: $A_{0}^{a}=\frac{1}{2}a^{2}$ Dies ist auch das Ergebnis der elementaren Rechnung (siehe oben).

Für die Fläche $A_{a}^{b}=A_{0}^{b}-A_{0}^{a}$ mit b > a ergibt sich entsprechend:

$A_{a}^{b}=\frac{1}{2}b^{2}-\frac{1}{2}a^{2}$

Für die mathematisch Interessierteren folgt nun noch ein strenger Beweis, dass gilt:

$1+2+...+n=\sum\limits_{ν=1}^{n}ν=\frac{n(n+1)}{2}$ 

Es gilt: $\sum\limits_{ν=1}^{n}[(ν+1)^2-ν^2]=(n+1)^2-1$ (Schreibe die Summanden der Reihe nach auf, nur $(n+1)^{2}$ und $-1^{2} = -1$ bleiben übrig.)

Daraus folgt: $\sum\limits_{ν=1}^{n}(ν^2+2ν+1-ν^2)=n^2+2n+1-1$ (zweimaliges Anwenden der 1. Binomischen Formel)

$\Leftrightarrow \sum\limits_{ν=1}^{n}(2ν+1)=n^2+2n$ (klar)

$\Leftrightarrow \sum\limits_{ν=1}^{n}2ν+\sum\limits_{ν=1}^{n}1=n^2+2n$ (klar)

Es gilt:

$\sum\limits_{ν=1}^{n}1=\sum\limits_{ν=1}^{n}1⋅ν^{0}=1⋅1^{0}+1⋅2^{0}+...+1⋅n^{0}=1⋅1+1⋅1+...+1⋅1=1+1+...+1$

Die 1 kommt n-mal vor, also ist $\sum\limits_{ν=1}^{n}1=n$. Damit folgt:

$2\sum\limits_{ν=1}^{n}ν+n=n^2+2n$

$\Leftrightarrow 2\sum\limits_{ν=1}^{n}ν=n^2+n$ (Auf beiden Seiten -n)

$\Leftrightarrow \sum\limits_{ν=1}^{n}ν=\frac{n^2+n}{2}=\frac{n(n+1)}{2}$ (Auf beiden Seiten /2)

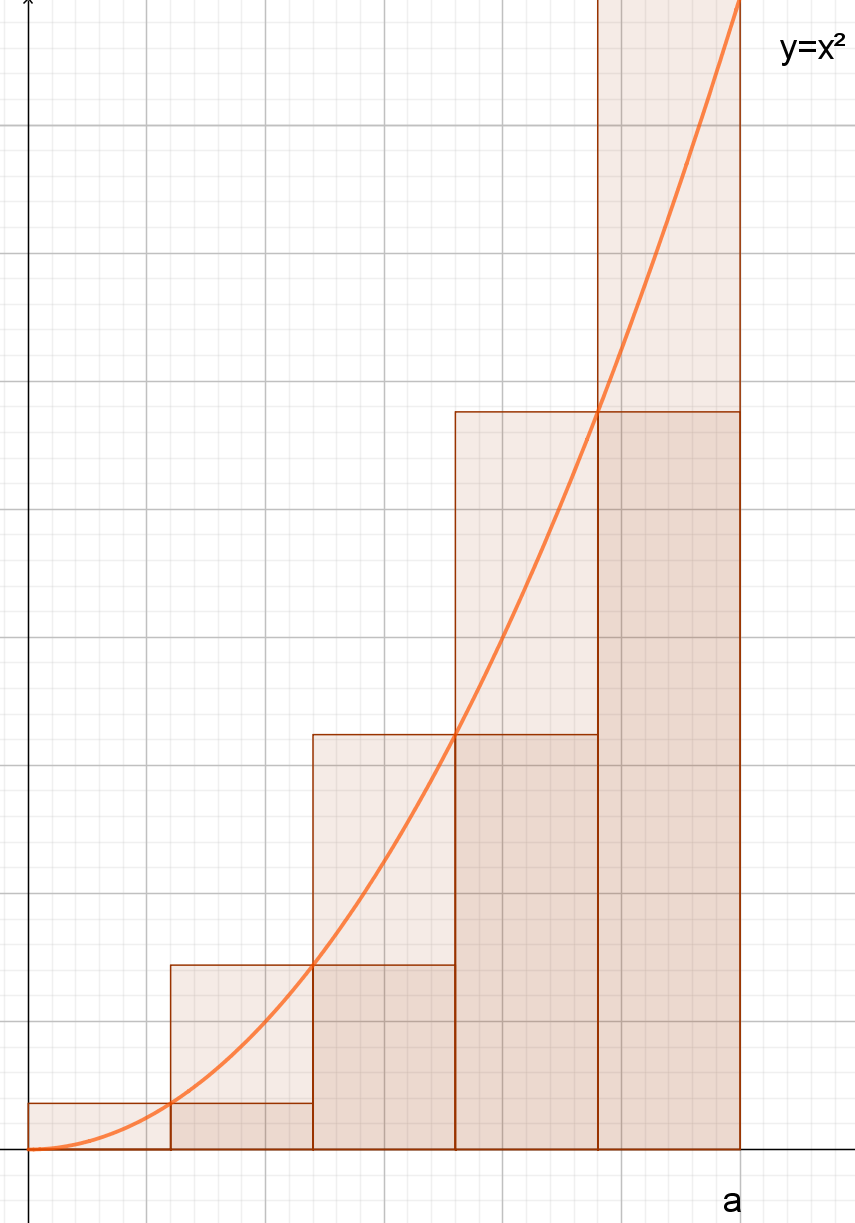
Die Normalparabel y=x² schließt mit der x-Achse und der Geraden x = a mit a > 0 eine endliche Fläche ein. Dieser Flächeninhalt $A_{0}^{a}$ ist mit Hilfe der Streifenmethode zu bestimmen.

Breite der Rechtecke: $h=Δx=\frac{a}{n}$

Höhe der Rechtecke: Funktionswerte an den Rechtecksenden, z. B. $f(2h)=4h^{2}$

Für die Obersumme gilt:

$S_{n} = h⋅h^{2}+h⋅(2h)^{2}+...+h⋅(nh)^{2}=h^{3}(1^{2}+2^{2}+...+n^{2})$

Für $1^{2}+2^{2}+...+n^{2}=\sum\limits_{ν=1}^{n}ν^2$ gibt es eine Berechnungsformel:

$\sum\limits_{ν=1}^{n}ν^2=\frac{n(n+1)(2n+1)}{6}$

Damit folgt $S_{n}=h^{3}⋅\frac{n(n+1)(2n+1)}{6}=\frac{a^{3}}{n^{3}}\frac{n^{3}(1+\frac{1}{n})(2+\frac{1}{n})}{6}$

Wer den letzten Schritt nicht versteht, für den gibt es einen Tipp: Klammere $n$ bei $(n+1)$ aus, dann klammere $n$ bei $(2n+1)$ aus. Ich hoffe, dass du jetzt verstehst, warum aus $n$ plötzlich $n^{3}$ wird. Und aus $(n+1)$ wird $(1+\frac{1}{n}$) und aus $(2n+1)$ wird $(2+\frac{1}{n})$.

Nun wird mit $n^{3}$ gekürzt: $S_{n}=a^{3}\frac{(1+\frac{1}{n})(2+\frac{1}{n})}{6}$ Daraus folgt für den Grenzwert:

$\lim\limits_{n\to\infty}S_{n}=\lim\limits_{n\to\infty}a^{3}\frac{(1+\frac{1}{n})(2+\frac{1}{n})}{6}=\frac{a^{3}}{6}\lim\limits_{n\to\infty}(1+\frac{1}{n})(2+\frac{1}{n})=\frac{a^{3}}{6}⋅1⋅2=\frac{a^{3}}{3}$

Nun folgt die etwas schwierigere Rechnung für die Untersumme:

$s_{n} = h⋅h^{2}+h⋅(2h)^{2}+...+h⋅[(n-1)⋅h]^{2}=h^{3}(1^{2}+2^{2}+...+(n-1)^{2})$

Wir haben es hier mit $\sum\limits_{ν=1}^{n-1}ν^2$ zu tun. Wir müssen also in die Formel $\frac{n(n+1)(2n+1)}{6}$ an der Stelle n einfach n-1 einsetzen. Wir erhalten also:

$\frac{(n-1)((n-1)+1)(2(n-1)+1)}{6}=\frac{(n-1)n(2n-1)}{6}=\frac{n(n-1)(2n-1)}{6}$ Für s_n erhalten wir damit:

$s_{n}=h^{3}\frac{n(n-1)(2n-1)}{6}=\frac{a^{3}}{n^{3}}\frac{n^{3}(1-\frac{1}{n})(2-\frac{1}{n})}{6}=\frac{a^{3}(1-\frac{1}{n})(2-\frac{1}{n})}{6}$

Daraus folgt für den Grenzwert: $\lim\limits_{n\to\infty}s_{n}=\frac{a^{3}}{3}$.

Damit haben wir: $A_{0}^{a}=\lim\limits_{n\to\infty}S_{n}=\lim\limits_{n\to\infty}s_{n}=\frac{a^{3}}{3}$

Für die Fläche $A_{a}^{b}$ mit b>a, also für $A_{a}^{b}=A_{0}^{b}-A_{0}^{a}$, ergibt sich somit:

$A_{a}^{b}=\frac{b^{3}}{3}-\frac{a^{3}}{3}$

Übung:

Berechne bezüglich $f: x→x^{2} A_{0}^{2}$

Lösungsweg: $A_{0}^{2}=\frac{1}{3}⋅2^{3}-\frac{1}{3}⋅0^{3}=\frac{8}{3}≈2,67$

Weitere Übungen:

Berechne:

1.) $A_{0,1}^{1,2}$ (Lösung: ≈0,58)

2.) $A_{0,5}^{2\sqrt{2}}$ (Lösung: ≈7,50)

Für die sehr Interessierten unter Euch folgt jetzt der schwierige Beweis, dass gilt:

$\sum\limits_{ν=1}^{n}ν^{2}=\frac{n(n+1)(2n+1)}{6}$

Ausgangspunkt ist die folgende Gleichung:

$\sum\limits_{ν=1}^{n}[(ν+1)^{3}-ν^{3}]=(n+1)^{3}-1$. Wenn du die Summanden der Reihe nach aufschreibst, wirst du feststellen, dass nur $(n+1)^{3}$ und $-1^{3}=-1$ übrigbleiben.

Im Folgenden werden nur noch die linke bzw. rechte Seite vereinfacht.

Zuerst die linke Seite:

$\sum\limits_{ν=1}^{n}[(ν+1)^{3}-ν^{3}]=\sum\limits_{ν=1}^{n}[ν^{3}+3ν^{2}+3ν+1-ν^{3}]$ Hier bleibt Dir nichts anderes übrig, als $(ν+1)^{3}=(ν+1)(ν+1)(ν+1)$ auszurechnen. Wiederhole dafür den Trick mit dem Pascalschen Dreieck!

$\sum\limits_{ν=1}^{n}[ν^{3}+3ν^{2}+3ν+1-ν^{3}]=\sum\limits_{ν=1}^{n}[3ν^{2}+3ν+1]$ (klar)

$\sum\limits_{ν=1}^{n}[3ν^{2}+3ν+1]=3⋅\sum\limits_{ν=1}^{n}ν^{2}+3⋅\sum\limits_{ν=1}^{n}ν+\sum\limits_{ν=1}^{n}1$ (Das Summenzeichen wird auf die einzelnen Summanden verteilt.)

Für $\sum\limits_{ν=1}^{n}ν$ gibt es eine Berechnungsformel, die wir schon benutzt und sogar bewiesen haben (siehe Reiter "Vertiefung 1"): Unser alter Bekannter $\frac{n(n+1)}{2}$. Auch wissen wir schon aus "Vertiefung 1", dass $\sum\limits_{ν=1}^{n}1=n$ ist.

Insgesamt folgt also für die linke Seite:

$\sum\limits_{ν=1}^{n}[3ν^{2}+3ν+1]=3⋅\sum\limits_{ν=1}^{n}ν^{2}+3⋅\frac{n(n+1)}{2}+n=3⋅\sum\limits_{ν=1}^{n}ν^{2}+\frac{3}{2}n^{2}+\frac{3}{2}n+n=3⋅\sum\limits_{ν=1}^{n}ν^{2}+\frac{3}{2}n^{2}+\frac{5}{2}n$

Nun die rechte Seite: $(n+1)^{3}-1=n^{3}+3n^{2}+3n+1-1=n^{3}+3n^{2}+3n$.

Wir erhalten also:

$3⋅\sum\limits_{ν=1}^{n}ν^{2}+\frac{3}{2}n^{2}+\frac{5}{2}n=n^{3}+3n^{2}+3n$

$\Leftrightarrow3⋅\sum\limits_{ν=1}^{n}ν^{2}=n^{3}+\frac{3}{2}n^{2}+\frac{1}{2}n$ (Auf beiden Seiten $-\frac{3}{2}n^{2}$ und $-\frac{5}{2}n$)

$\Leftrightarrow\sum\limits_{ν=1}^{n}ν^{2}=\frac{1}{3}(n^{3}+\frac{3}{2}n^{2}+\frac{1}{2}n)$ (Auf beiden Seiten :3)

$\Leftrightarrow\sum\limits_{ν=1}^{n}ν^{2}=\frac{1}{6}(2n^{3}+3n^{2}+n)$ (Bei der Klammer auf der rechten Seite der Gleichung wurde $\frac{1}{2}$ ausgeklammert.)

$\Leftrightarrow\sum\limits_{ν=1}^{n}ν^{2}=\frac{1}{6}n(2n^{2}+3n+1)$ (Bei der Klammer auf der rechten Seite der Gleichung wurde n ausgeklammert.)

Es gilt: $(n+1)(2n+1)=2n^{2}+n+2n+1=2n^{2}+3n+1$ Also folgt schließlich:

$\sum\limits_{ν=1}^{n}ν^{2}=\frac{1}{6}n(n+1)(2n+1)$

Wir vergleichen die bisherigen Ergebnisse:

$f(x)=1=x^{0} ⇒ A_{a}^{b}=b-a=\frac{b^{1}}{1}-\frac{a^{1}}{1}$ Denke hier an den Flächeninhalt des Rechtecks: Länge $(b-a)$ mal Breite $1$!

$f(x)=x=x^{1} ⇒ A_{a}^{b}=\frac{b^{2}}{2}-\frac{a^{2}}{2}$ (siehe Reiter "Fläche unter y=x")

$f(x)=x^{2} ⇒ A_{a}^{b}=\frac{b^{3}}{3}-\frac{a^{3}}{3}$ (siehe Reiter "Fläche unter der Normalparabel")

...

Dies lässt auf die folgende allgemeine Berechnungsformel schließen, die man auch beweisen kann:

$f(x)=x^{n} ⇒ A_{a}^{b}=\frac{b^{n+1}}{n+1}-\frac{a^{n+1}}{n+1}$. $A_{a}^{b}$ ist der Flächeninhalt zwischen dem Graphen der Funktion $f: x→x^{n}; n∈\mathbb{N}∧x∈\mathbb{R}_{0}^{+}$ über dem Intervall [a;b] mit b>a.

Beispielrechnungen:

Berechne bezüglich der Funktion $f: x→x^{3} A_{1}^{4}:$

Lösung: $A_{1}^{4}=\frac{4^{4}}{4}-\frac{1^{4}}{4}=\frac{255}{4}=63,75[FE]$

Berechne bezüglich der Funktion $f: x→x^{5} A_{2}^{3}:$

Lösung: $A_{2}^{3}=\frac{3^{6}}{6}-\frac{2^{6}}{6}=\frac{665}{6}≈110,83[FE]$

Übungen

1.) Berechne bezüglich $f: x→x^{3} A_{1}^{2}$ (Lösung: 3,75)

2.) Berechne bezüglich $f: x→x^{3} A_{\frac{2}{3}}^{\frac{5}{3}}$ (Lösung: ≈1,88)

Zusatzaufgabe: Für die sehr Interessierten unter Euch gibt es noch folgende Aufgabe: Bestimme den Flächeninhalt unter der kubischen Funktion $f: x→x^{3}$ über dem Intervall [0;a] mittels Grenzwertbildung der entsprechenden Ober- und Untersumme.

Hilfe: Während der Rechnung stößt du auf das Problem 1³+2³+...+n³, also die Summe der Kubikzahlen, zu berechnen. Glücklicherweise gibt es auch hier eine Berechnungsformel: $\sum\limits_{ν=1}^{n}ν^{3}=\frac{n^{2}⋅(n+1)^{2}}{4}$

(Lösung: $A_{0}^{a}=\frac{1}{4}a^{4}$)

In der Integralrechnung bist du jetzt schon sehr weitgekommen. Jetzt ist es nicht mehr weit bis zur Einführung des Integralbegriffs, dem Erarbeiten des wichtigen Hauptsatzes der Differential- und Integralrechnung und dem Erlernen vieler Rechenregeln für die Integration. Viel Erfolg auf diesem Weg!