Zunächst wird dir erklärt, wie das Kepler-Fernrohr, auch astronomisches Fernrohr genannt, funktioniert. Es wurde zwar später als das Galilei-Fernrohr konstruiert (siehe Reiter Geschichte), aber die Funktionsweise ist beim Kepler-Fernrohr leichter zu verstehen. In der folgenden Darstellung wird das Bild eines weit entfernten Gegenstands mittels des Kepler-Fernrohrs konstruiert: 

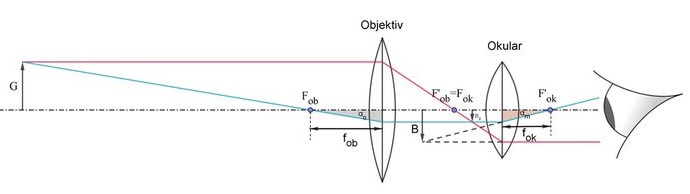
Ganz allgemein formuliert, musst du dir Folgendes merken:

Das Objektiv erzeugt von einem fernen Gegenstand ein reelles Zwischenbild. Dieses wird durch das Okular wie mit einer Lupe betrachtet.

Da du unbedingt die Konstruktion verstehen und nachzeichnen solltest, folgt eine ausführliche Konstruktionsbeschreibung:

Nehme ein DIN A4 Blatt quer. Beginne mit dem Zeichnen der strichpunktierten optischen Achse. Zeichne möglichst am linken Rand einen 2 cm hohen Pfeil. Dieser Pfeil ist der Gegenstand. 15 cm weiter nach rechts zeichne die Mittelebene der Objektivlinse mit der Brennweite $f_{ob} = 3\ cm$. Zeichne die Brennpunkte $F_{ob}$ und $F'_{ob}$. 5 cm von der Mittelebene der Objektivlinse entfernt zeichne die Mittelebene der Okularlinse mit der Brennweite $f_{ok} = 2\ cm$. Zeichne die Brennpunkte $F_{ok}$ und $F'_{ok}$. Dabei stellst du fest, dass $F'_{ob}$ und $F_{ok}$ zusammenfallen. Ganz rechts zeichne ein Auge ein. Jetzt beginnt die eigentliche Konstruktion des Bildes: Beginne mit dem roten Lichtstrahl: Er verläuft zunächst parallel zur optischen Achse, er wird vom Objektiv so gebrochen, dass er durch den Brennpunkt $F'_{ob}$ läuft. Da die Brennpunkte $F'_{ob}$ und $F_{ok}$ zusammenfallen, verläuft der Strahl nach der Brechung durch das Okular wieder parallel zur optischen Achse. Der hellblaue Lichtstrahl geht zunächst durch den Brennpunkt $F_{ob}$ und wird vom Objektiv so gebrochen, dass er parallel zur optischen Achse läuft. Dort, wo sich der rote und der hellblaue Strahl schneiden, entsteht das reelle Zwischenbild $B_{z}$ der Pfeilspitze. Das Zwischenbild des Pfeils ist also verkleinert, reell, auf dem Kopf stehend und seitenverkehrt. Der hellblaue Strahl wird schließlich so durch das Okular gebrochen, dass er durch den Brennpunkt $F'_{ok}$ läuft. Es entsteht also insgesamt ein divergentes Lichtbündel mit dem hellblauen und roten Strahl als Randstrahlen, das ins Auge gelangt. Unser menschliches Auge geht immer von einer geradlinigen Lichtausbreitung aus, so dass der hellblaue und der rote Strahl nach links verlängert werden (siehe die gestrichelten Linien in der obigen Darstellung). Dort, wo sich die gestrichelten Linien schneiden, entsteht schließlich das virtuelle Bild B der Pfeilspitze. Insgesamt entsteht ein virtuelles, verkleinertes, auf den Kopf stehendes und seitenverkehrtes Bild des Pfeils. Gratulation, du hast die Konstruktion geschafft. Wenn dir nicht gleich alles beim ersten Mal gelungen ist, dann führe die Konstruktion ein zweites Mal durch. Je mehr du übst, desto sicherer und schneller wirst du bei der Bildkonstruktion.

Du freust dich bestimmt über deine gelungene Konstruktion, aber du bist sicher enttäuscht von dem Ergebnis: Der ganze Aufwand nur für ein verkleinertes und virtuelles Bild!!! Das stimmt zwar, aber schaue genauer auf die obige Darstellung: Der Sehwinkel, unter dem man ein Objekt sieht, und er spielt hier die Hauptrolle, hat sich von $α_{o}$ (o wie ohne Gerät) auf $α_{m}$ (m wie mit Gerät) vergrößert. Der Sehwinkel bestimmt nämlich die Größe des Nethautbildes.

In der folgenden Darstellung ist die Bildentstehung bei einem unendlich weit entfernten Objekt wie z. B. bei einem Stern mit schräg einfallenden zueinander parallelen Strahlen dargestellt:

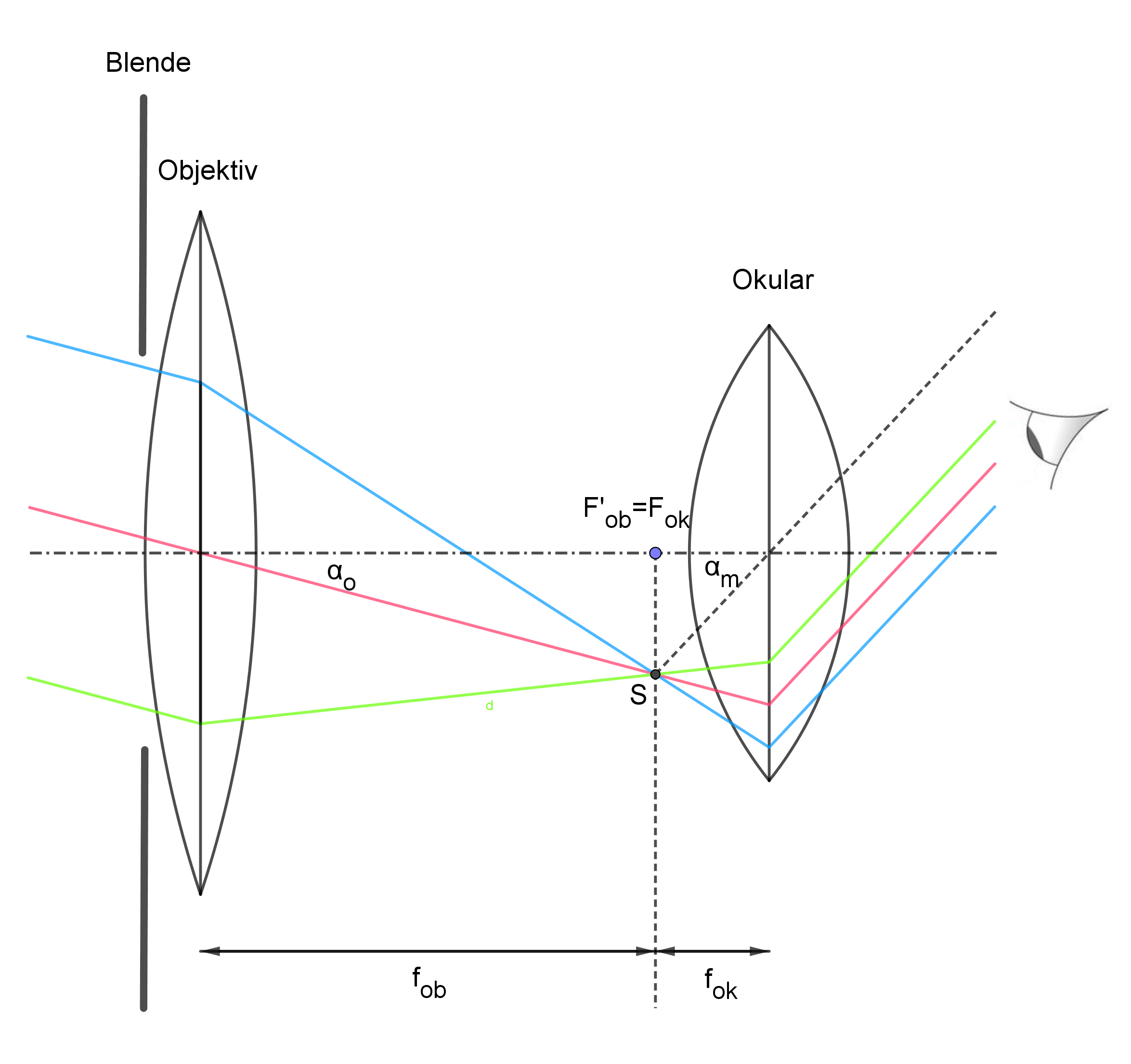
Du erkennst, dass die zueinander parallel einfallenden Strahlen auch nach dem Durchgang durch das Fernrohr parallel ins Auge gelangen und sich dabei der Sehwinkel deutlich vergrößert hat.

Die Vergrößerung kann man sogar berechnen: Dazu schaue dir die obigen Darstellungen genau an. Du erkennst, dass $α_{o}$ dem Verhältnis $\frac{B_{z}}{f_{ob}}$ und $α_{m}$ dem Verhältnis $\frac{B_{z}}{f_{ok}}$ entspricht. Also beträgt die Winkelvergrößerung $V=\frac{α_{m}}{α_{o}}=\frac{\frac{B_{z}}{f_{ok}}}{\frac{B_{z}}{f_{ob}}}=\frac{B_{z}}{f_{ok}}⋅\frac{f_{ob}}{B_{z}}=\frac{f_{ob}}{f_{ok}}$. Die Fernrohrlänge ist leichter zu berechnen: Da $F'_{ob}$ und $F_{ok}$ zusammenfallen, beträgt der Abstand des Objektivs zum Okular $f_{ob}+f_{ok}$ und das ist auch die Fernrohrlänge. Merke also:

Die Vergrößerung eines Kepler-Fernrohrs beträgt $V=\frac{f_{ob}}{f_{ok}}$ und die Länge beträgt $l=f_{ob}+f_{ok}$.

Um die chromatische und sphärische Abberation zu verhindern, besteht sowohl das Objektiv als auch das Okular aus Linsensystemen. Des Weiteren ist darauf zu achten, dass die Objektivlinse genügend groß ist, damit genügend Licht in das Fernrohr eindringen kann. Mit einem guten Stativ und einem Suchfernrohr ausgestattet, ist das astronomische Fernrohr nun fertig. Wie man das Kepler-Fernrohr auch für Beobachtungen auf der Erde einsetzen kann, erfährst du unter dem nächsten Reiter.