In diesem Reiter wird dir das Holländische oder Galileische Fernrohr vorgestellt, das noch vor dem Kepler-Fernrohr (siehe Reiter Geschichte) entwickelt wurde. Es hat wie das Kepler-Fernrohr als Objektivlinse eine langbrennweitige Sammellinse, aber im Unterschied zum Kepler-Fernrohr ist die Okularlinse eine kurzbrennweitige Zerstreuungslinse. Die Brennpunkte von Objektiv und Okular fallen auf der Beobachterseite zusammen, also: $F'_{ob}=F_{ok}$. In der folgenden Darstellung ist die Bildentstehung eines weit entfernten Gegenstandes dargestellt:

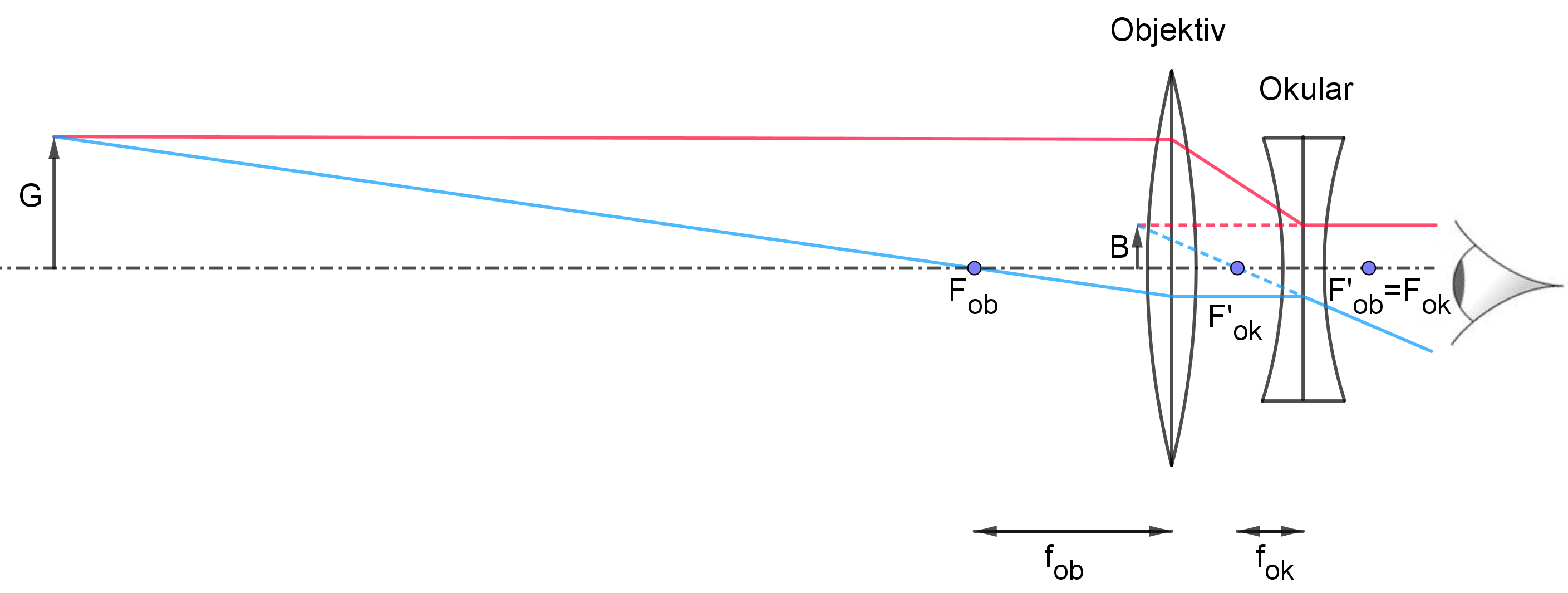
Es entsteht ein virtuelles, verkleinertes, aufrechtes und seitenrichtiges Bild des Gegenstandes. Für Erdbeobachtungen ist das ein großer Vorteil. Man benötigt keine zusätzlichen Bauteile für die Bildumkehr. Allerdings ist das Sichtfeld viel kleiner als beim Kepler-Fernrohr. Auch beim Galilei-Fernrohr ist wie beim Kepler-Fernrohr $α_{m}$ größer als $α_{o}$.

Im unteren Bild ist die Bildkonstruktion mit schräg einfallenden zueinander parallelen Strahlen eines "unendlich" weit entfernten Sterns dargestellt:

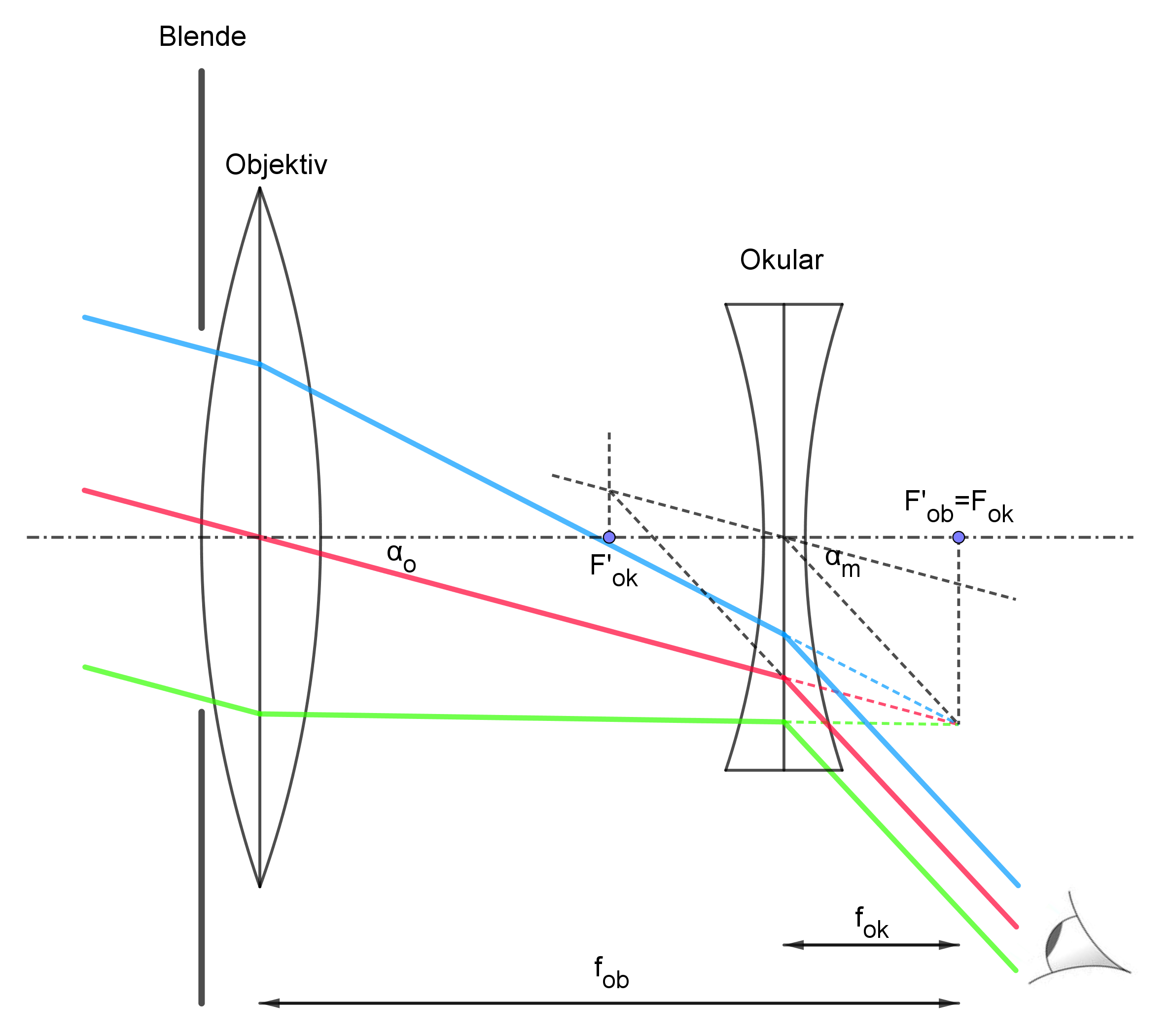
Merke Folgendes:

Die Vergrößerung eines Galilei-Fernrohrs beträgt $V=\frac{f_{ob}}{|f_{ok}|}$ und die Länge beträgt $l=f_{ob}-|f_{ok}|$.

Im obigen Merksatz steht $f_{ok}$ in Betragstrichen, da die Brennweite einer Zerstreuungslinse ein negatives Vorzeichen hat. Das Galilei-Fernrohr ist also kleiner als ein Kepler-Fernrohr mit gleicher Vergrößerung. Aber wegen des kleinen Sichtfeldes wird es heute weniger für astronomische Zwecke genutzt, sondern am häufigsten als Opernglas (siehe oben erstes Bild).