Die Bernoulli-Formel
Darf Robin Hood Maid Marian heiraten?

Nottingham an einem schönen und windstillen Sommertag im Jahr 1223: Der Sheriff von Nottingham hat Robin Hood aus dem Sherwood Forest zum Bogenschießen eingeladen und ihm Folgendes angeboten: Robin schießt dreimal auf eine 600 Fuß (das sind ca. 183 m) entfernte Zielscheibe. Wenn er mindestens zweimal das Zentrum der Zielscheibe trifft, darf er seine Freundin Maid Marian heiraten. Wenn nicht, wird der Sheriff der Bräutigam sein. Soll Robin auf das Angebot eingehen? Du wirst ihm bei der Entscheidungsfindung helfen und dein bisheriges Wissen über die Wahrscheinlichkeitsrechnung anwenden.
Robin ist der beste Bogenschütze Englands und hat trotz der großen Entfernung von 600 Fuß eine Trefferwahrscheinlichkeit von 70%. Robin ist in seinen besten Jahren und auch beim zweiten und dritten Schuss bleibt die Trefferwahrscheinlichkeit konstant. Du erkennst, dass es sich hier um eine Bernoulli-Kette handelt. Dabei ist n=3 und p=70%=0,7.
Robin darf heiraten, wenn er mindestens zweimal das Zentrum der Zielscheibe trifft, das heißt, wenn er zweimal oder dreimal trifft. Um die Wahrscheinlichkeiten für zwei oder drei Treffer zu berechnen, zeichnen wir ein Baumdiagramm (Dabei bedeutet T=Treffer und N=Nichttreffer oder Niete):
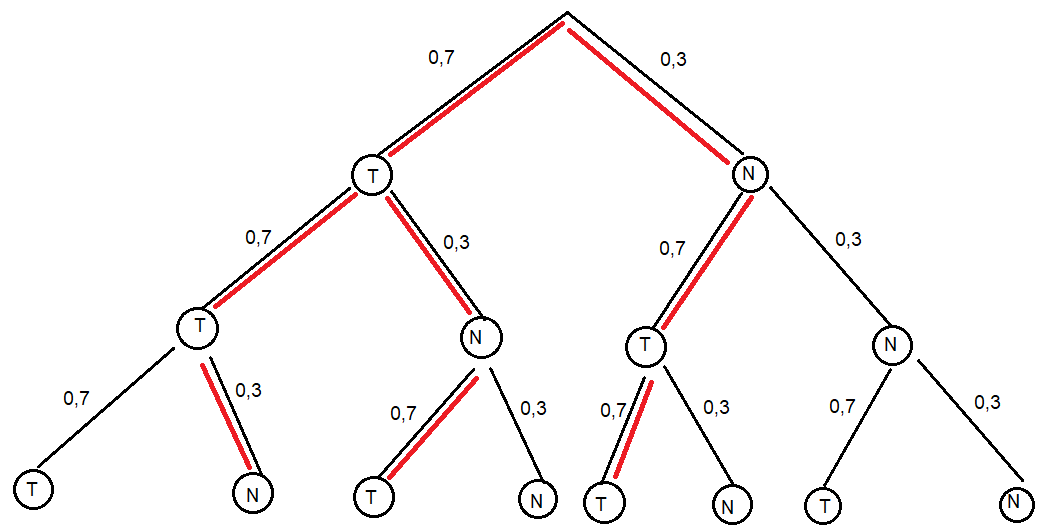
Die Wahrscheinlichkeit für drei Treffer lässt sich schnell ablesen: $\mathrm{P(„drei\,Treffer”)=0,7^{3}=0,343}$.
Jetzt berechnen wir die Wahrscheinlichkeit für zwei Treffer: Jeder Pfad mit zwei Treffern (im obigen Baumdiagramm rot markiert) hat die Pfadwahrscheinlichkeit von $\mathrm{0,7^{2}·0,3^{1}=0,147}$. Insgesamt gibt es drei Pfade mit genau zwei Treffern. Also gilt: $\mathrm{P(„zwei\,Treffer”)=3·0,147=0,441}$.
Jetzt müssen wir nur noch addieren: $\mathrm{P(„mindestens\,zwei\,Treffer”)=P(„zwei\,Treffer”)+P(„drei\,Treffer”)}$
$\mathrm{=0,441+0,343=0,784=78,4\%}$.
Du kannst also ruhigen Gewissens Robin empfehlen, auf den Vorschlag des Sheriffs einzugehen.
Stelle dir vor, dass Robin hätte 10 mal schießen müssen. Das Zeichnen eines Baumdiagrammes wäre jetzt sehr mühsam. Deshalb versuchen wir, eine Formel für die Wahrscheinlichkeit zu finden, mit der Robin genau k mal trifft. Wir bleiben bei 3 Schüssen für die folgenden Überlegungen:
Wir führen eine Zufallsvariable X ein, die die Anzahl der Treffer kennzeichnet, und wir berechnen $\mathrm{P(X=k)}$. Die Wahrscheinlichkeit für einen Pfad lässt sich leicht berechnen: Sie ist für einen Pfad der Länge $\mathrm{3}$ mit genau $\mathrm{k}$ Treffern und entsprechend $\mathrm{3-k}$ Nichttreffern: $\mathrm{0,7^{k}·0,3^{3-k}}$. Aber wie kommen wir darauf, dass es genau drei Pfade für $\mathrm{k=2}$ gibt, ohne ein Baumdiagramm benutzen zu müssen? Hier musst du dein Kombinatorik-Wissen anwenden: Es gibt nämlich genau $\mathrm{{3}\choose{2}}=3$ Kombinationen, 2 Treffer auf 3 Positionen verteilen zu können. Also gibt es $\mathrm{{3}\choose{k}}$ Pfade für $\mathrm{k}$ Treffer. Jetzt haben wir alle Zutaten für die Formel zusammengestellt: Es gilt: $\mathrm{P(X=k)={{3}\choose{k}}·0,7^{k}·0,3^{3-k}}$. Nun kannst du ganz leicht die restlichen Trefferwahrscheinlichkeiten ohne Baumdiagramm bestimmen:
Wahrscheinlichkeit für genau $\mathrm{0}$ Treffer: $\mathrm{P(X=0)={{3}\choose{0}}·0,7^{0}·0,3^{3}=1·1·0,3^{3}=0,027}$.
Wahrscheinlichkeit für genau $\mathrm{1}$ Treffer: $\mathrm{P(X=1)={{3}\choose{1}}·0,7^{1}·0,3^{2}=3·0,7·0,3^{2}=0,189}$.
Für die Berechnung des Binomialkoeffizienten $\mathrm{{{n}\choose{k}}}$ musst du nicht mit der komplizierten Formel $\mathrm{\frac{n!}{k!·(n-k)!}}$ arbeiten, sondern du kannst auf deinem Taschenrechner "nCr" benutzen (auf den meisten Taschenrechnern mittel SHIFT und der Geteilt-Taste auswählbar). Und du kannst dir merken, dass $\mathrm{{{n}\choose{0}}=1}$ und $\mathrm{{{n}\choose{n}}=1}$ ist. Das erleichtert das Rechnen sehr.
Im Folgenden stellen wir die Wahrscheinlichkeiten für alle möglichen Trefferanzahlen in Form einer Tabelle zusammen und zeichnen das dazugehörige Histogramm:
| k | $\mathrm{P(X=k)}$ |
| 0 | 0,027 |
| 1 | 0,189 |
| 2 | 0,441 |
| 3 | 0,343 |
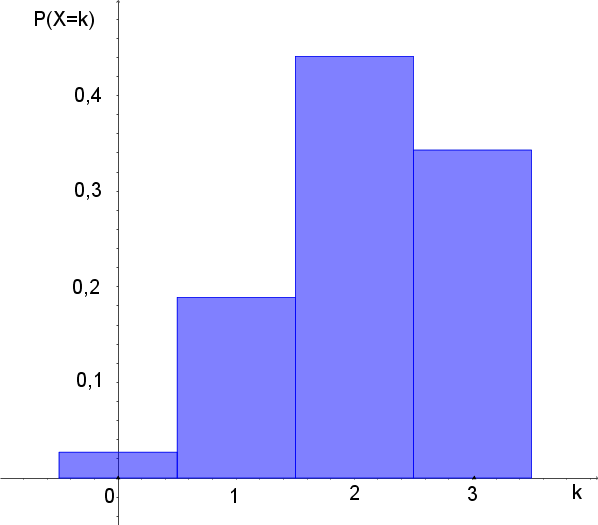
Du kannst leicht nachrechnen, dass die Summe aller Trefferanzahlwahrscheinlichkeiten $\mathrm{1}$ ist, und du siehst deutlich anhand des Histogramms, dass das Maximum der Wahrscheinlichkeit bei 2 Treffern liegt.
Da die Anzahl der Pfade für eine bestimmte Anzahl von Treffern mittels des Binomialkoeffizienten berechnet werden kann, nennt man die Trefferanzahl $\mathrm{X}$ in einer Bernoulli-Kette eine binomialverteilte Zufallsvariable.
Wir können nun die Binomialverteilung definieren:
Die Anzahl X der Treffer in einer Bernoulli-Kette der Länge n ist eine Zufallsvariable, die die Werte 0 bis n annehmen kann. Die Wahrscheinlichkeitsverteilung von X wird Binomialverteilung genannt.
Wir verallgemeinen jetzt die oben hergeleitete Formel so, dass n-mal geschossen wird, d. h., unsere Bernoulli-Kette hat jetzt die Länge n. Die Trefferwahrscheinlichkeit pro Schuss ist jetzt p und die Nietenwahrscheinlichkeit entsprechend 1-p. Dann gilt:
$\mathrm{P(X=k)={{n}\choose{k}}·p^{k}·(1-p)^{n-k}}$.
Die Formel wird die Formel von Bernoulli oder kurz Bernoulli-Formel genannt.
Die Wahrscheinlichkeit für k Treffer bei einer binomialverteilten Zufallsvariable wird auch als $\mathrm{B(n;p;k)}$ seltener auch als $\mathrm{B_{n,p}(k)}$ bezeichnet. Auf den folgenden Reitern wird immer die erste Bezeichnung verwendet.
