Nun entwickeln wir eine Formel für den Umfang mittels umbeschriebener Polygone:

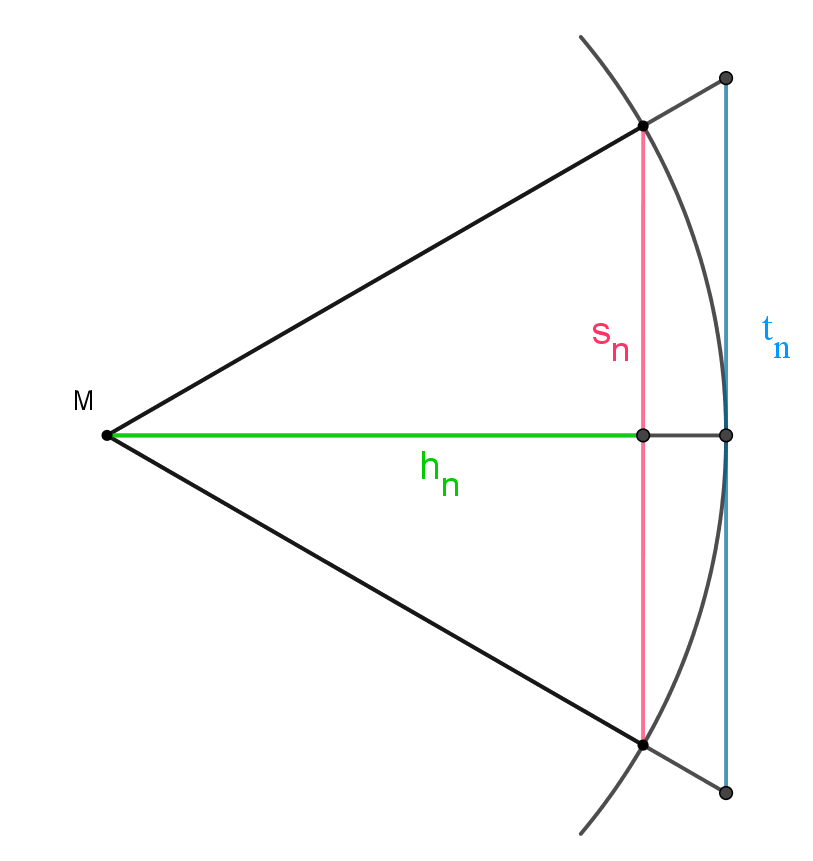
In der oberen Skizze ist $s_{n}$ wie im vorherigen Reiter eine Seite des einbeschriebenen n-Ecks. Hinzu kommt jetzt die Seite des umbeschriebenen n-Ecks namens $t_{n}$. Der Radius ist weiterhin 1.

Aus dem Strahlensatz folgt: $\frac{t_{n}}{s_{n}} = \frac{1}{h_{n}} ⇔ t_{n} = \frac{s_{n}}{h_{n}} (1) $

Für die grüne Seite $h_{n}$ gilt nach dem Satz des Pythagoras: $h_{n}^{2} = 1 - (\frac{s_{n}}{2})^2 ⇔ h_{n}=\sqrt{\frac{4 - s_{n}^{2}}{4}} ⇔ h_{n} = \frac{1}{2}\sqrt{4 - s_{n}^{2}}  (2) $

Nun setzen wir (2) in (1) ein und erhalten damit für $t_{n}$: $\underline{t_{n} = \frac{2⋅s_{n}}{\sqrt{4 - s_{n}^{2}}}}$

Für den Umfang des umbeschriebenen n-Ecks gilt entsprechend $\underline{U_{n} = n ⋅ t_{n} = n ⋅ \frac{2⋅s_{n}}{\sqrt{4 - s_{n}^{2}}}}$ 

Im folgendem Reiter werden wir schließlich die hergeleiteten Formeln in Excel nutzen, um die Zahl pi zu approximieren.