Im unteren Bild siehst du ein rechtwinkliges Dreieck ABC mit den Katheten a und b und der Hypotenuse c. Über die Seiten sind die Quadrate $\mathrm{a^{2}}$, $\mathrm{b^{2}}$ und $\mathrm{c^{2}}$ dargestellt.

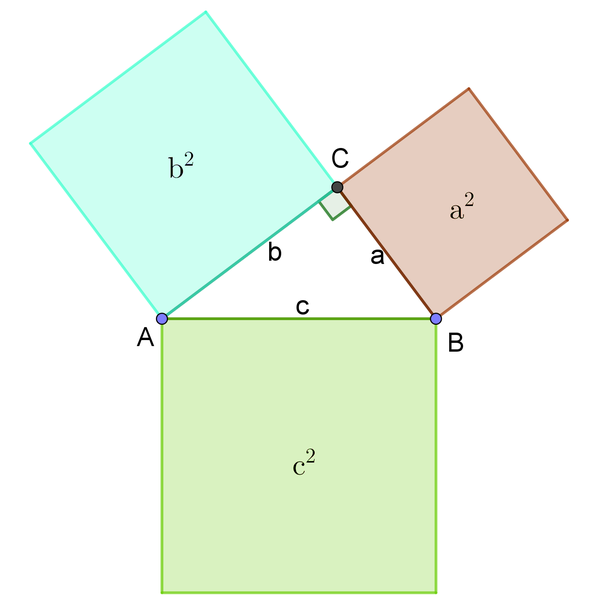
Du kannst schon nach Augenmaß vermuten, dass $\mathrm{a^{2}+b^{2}=c^{2}}$ gilt. In Worten: In einem rechtwinkligen Dreieck ist die Summe der Flächeninhalte der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrats.

Für den Satz des Pythagoras gibt es über 400 Beweise. Er gilt damit als der meistbewiesene Satz. Jetzt folgt ein einfacher geometrischer Beweis:

Zeichne dazu zunächst die untere Beweisfigur nach. Benutze z. B. folgende Längen: $\mathrm{a=4\,cm}$ und $\mathrm{b=3\,cm}$.

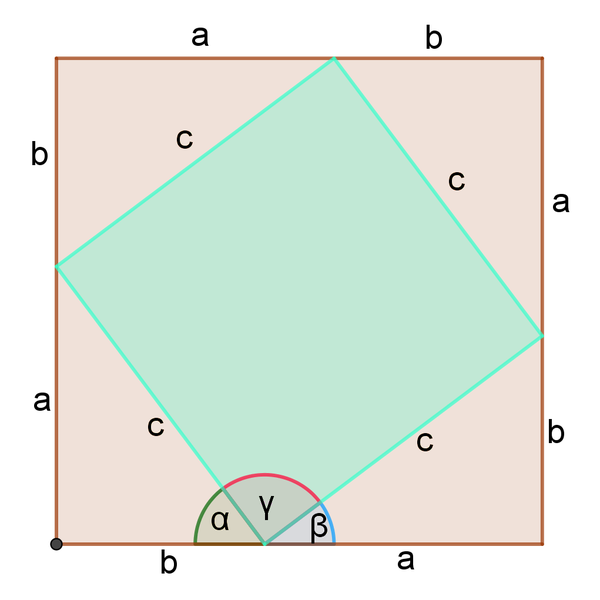
Das große Quadrat hat eine Seitenlänge von $\mathrm{a+b}$ und damit einen Flächeninhalt von $\mathrm{(a+b)^{2}=a^{2}+2⋅a⋅b+b^{2}}$. Es gibt noch eine weitere Möglichkeit, den Flächninhalt zu berechnen: Das große Quadrat setzt sich aus der blauen Raute mit der Länge c und vier rechtwinkligen Dreiecken mit den Katheten a und b und der Hypotenuse c zusammen.

Jetzt wird gezeigt, dass die Raute sogar ein Quadrat ist: Für die Winkelsumme in den rechtwinkligen Dreiecken gilt jeweils $\mathrm{α+β+90°=180°}$. Also gilt: $\mathrm{α+β=90°}$. Weiter gilt (siehe Beweisfigur): $\mathrm{α+β+γ=180°}$, denn die drei Winkel bilden einen gestreckten Winkel. Also folgt: $\mathrm{90°+γ=180°}$ und schließlich $\mathrm{γ=90°}$. Wenn ein Winkel einer Raute 90° groß ist, dann sind alle Winkel 90° groß. Die Raute ist also ein Quadrat mit der Seitenlänge c.

Nun kann man den Flächeninhalt des großen Quadrats auch wie folgt ausrechnen: $\mathrm{4⋅A_{rechtwinklige Dreiecke}+A_{blaues Quadrat}=4⋅\frac{a⋅b}{2}+c^{2}=2⋅a⋅b+c^{2}}$.

Beide Formeln für den Flächeninhalt des großen Quadrats werden jetzt gleichgesetzt:

$\mathrm{a^{2}+2⋅a⋅b+b^{2}=2⋅a⋅b+c^{2}\quad|-2⋅a⋅b}$

$\mathrm{a^{2}+b^{2}=c^{2}}$. Das sollte bewiesen werden. Der Beweis ist jetzt abgeschlossen.

Es gilt sogar die Umkehrung: Wenn in einem Dreieck $\mathrm{a^{2}+b^{2}=c^{2}}$ gilt, dann ist das Dreieck rechtwinklig.

Es gibt zahlreiche Anwendungen für den Satz des Pythagoras.  Aber die Quadratur eines Rechtecks ist mit dem Satz des Pythagoras nicht möglich, da in $\mathrm{a^{2}+b^{2}=c^{2}}$ nur Quadrate und kein Rechteck mit verschiedenen Längen vorkommen. Der Satz des Pythagoras dient in diesem Lernpfad als Basis und Beweismittel für die folgenden Sätze, mit denen die Quadratur möglich ist.