Die trigonometrischen Funktionen spielen eine sehr große Rolle in der Mathematik und Physik. Deshalb solltest du wissen, welchen Einfluss die Parameter auf die trigonometrischen Funktionen haben. Dies lernst du in diesem Lernpfad.

Auf den folgenden Reitern findest du nur Beispiele bezüglich der Sinusfunktion. Du kannst aber deine Erkenntnisse 1:1 auf die Cosinusfunktion übertragen. Leider verhält sich die Tangensfunktion ganz anders.

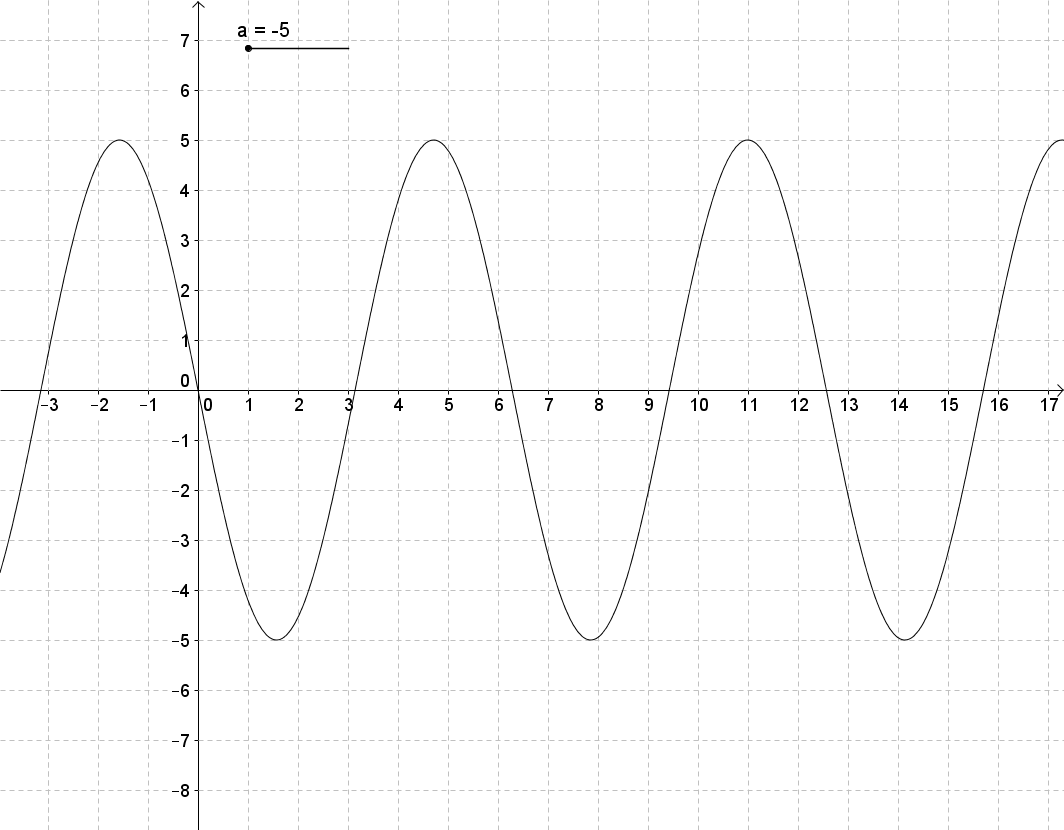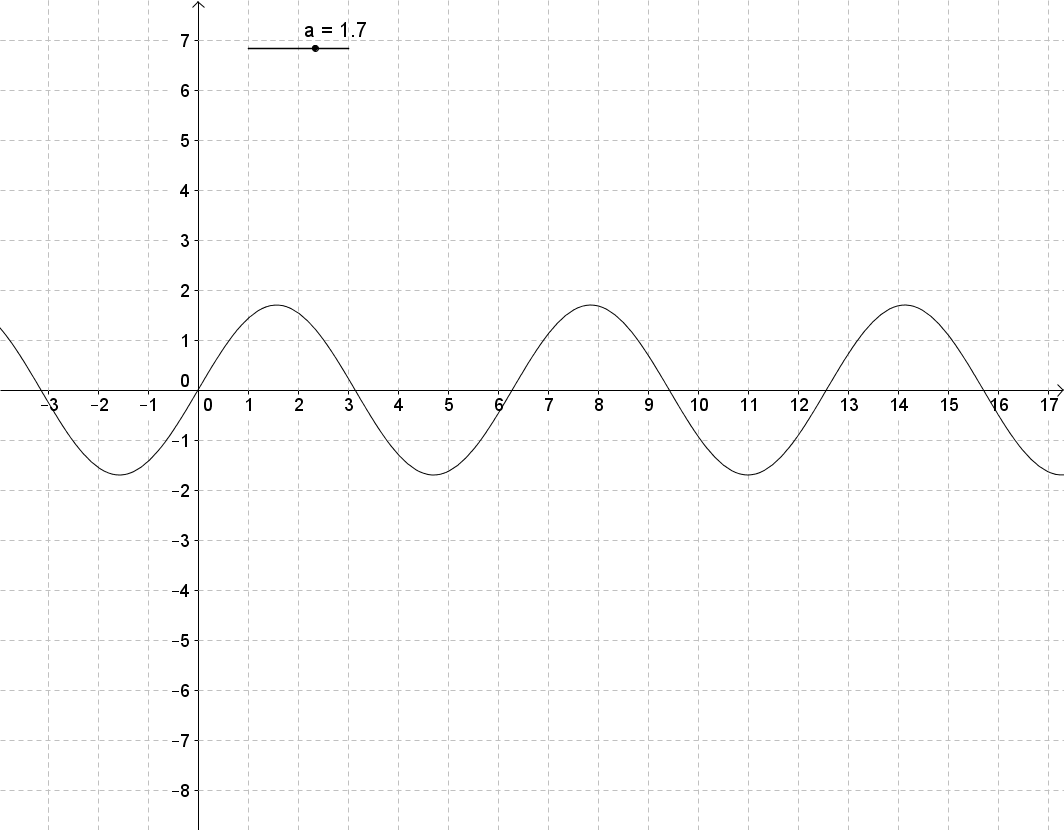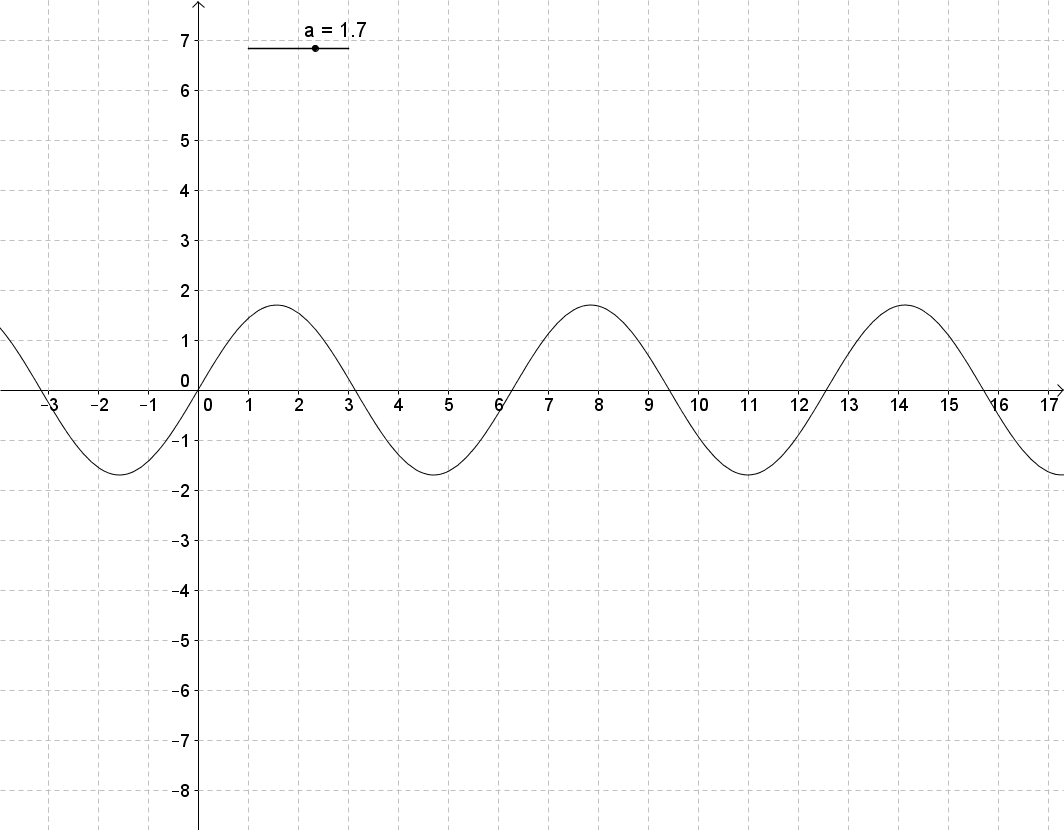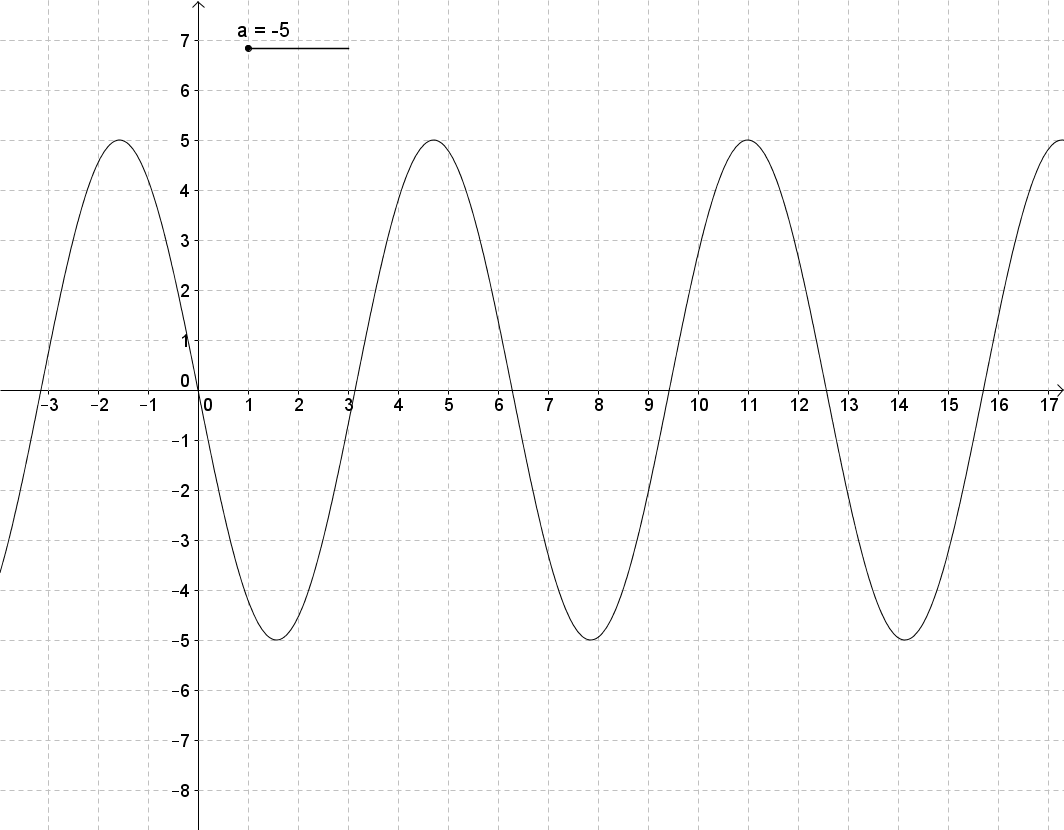
Beobachte, wie sich der Graph der Sinusfunktion y = a*sin(b*x+c)+d (mit b=1, c=0, d=0) ändert, wenn sich der Parameter a ändert. Schreibe deine Beobachtungsergebnisse so ausführlich wie möglich auf, und vergleiche mit der Lösung in dem entsprechendem Abschnitt auf dem Reiter "Lösungen".

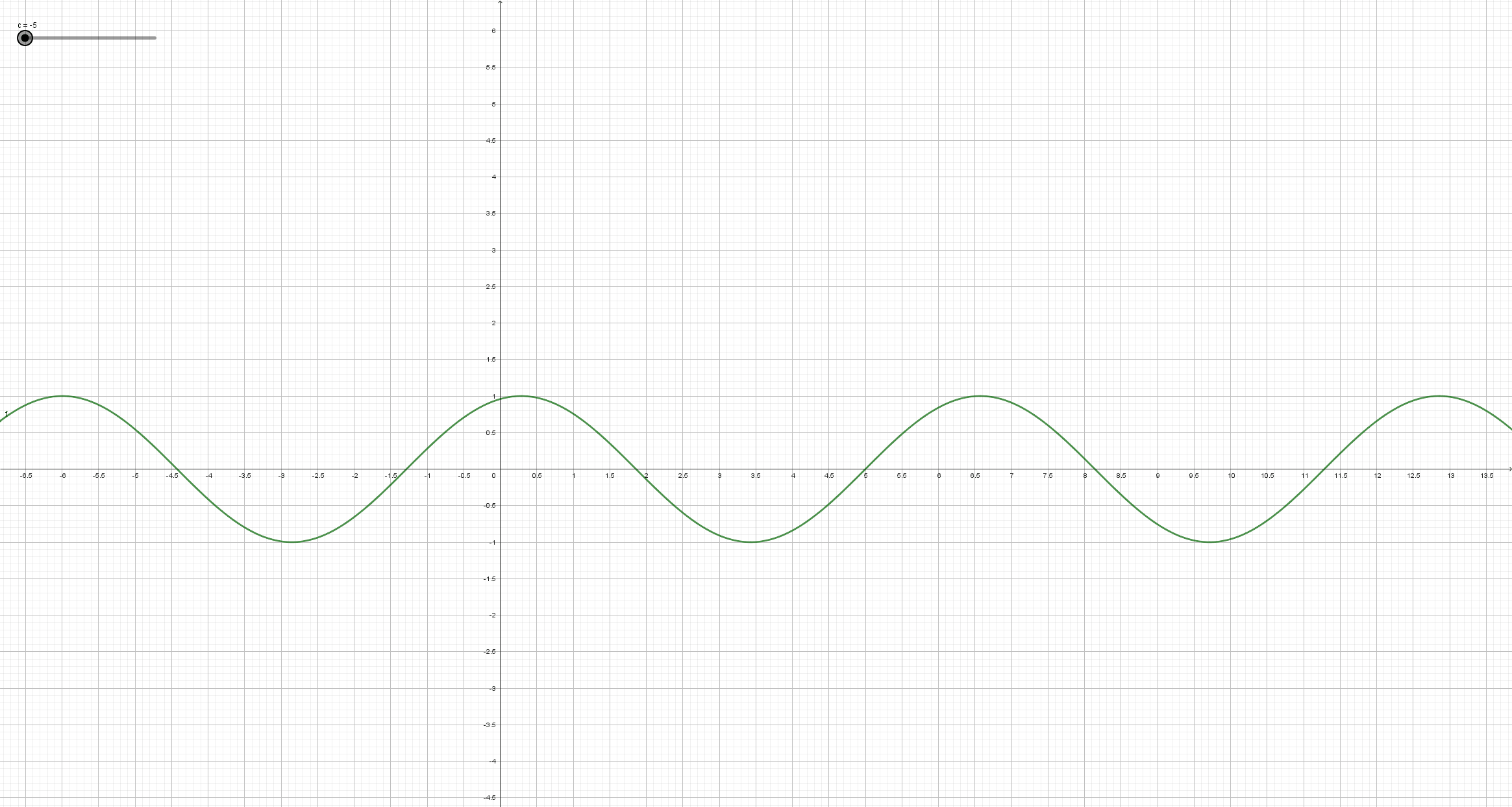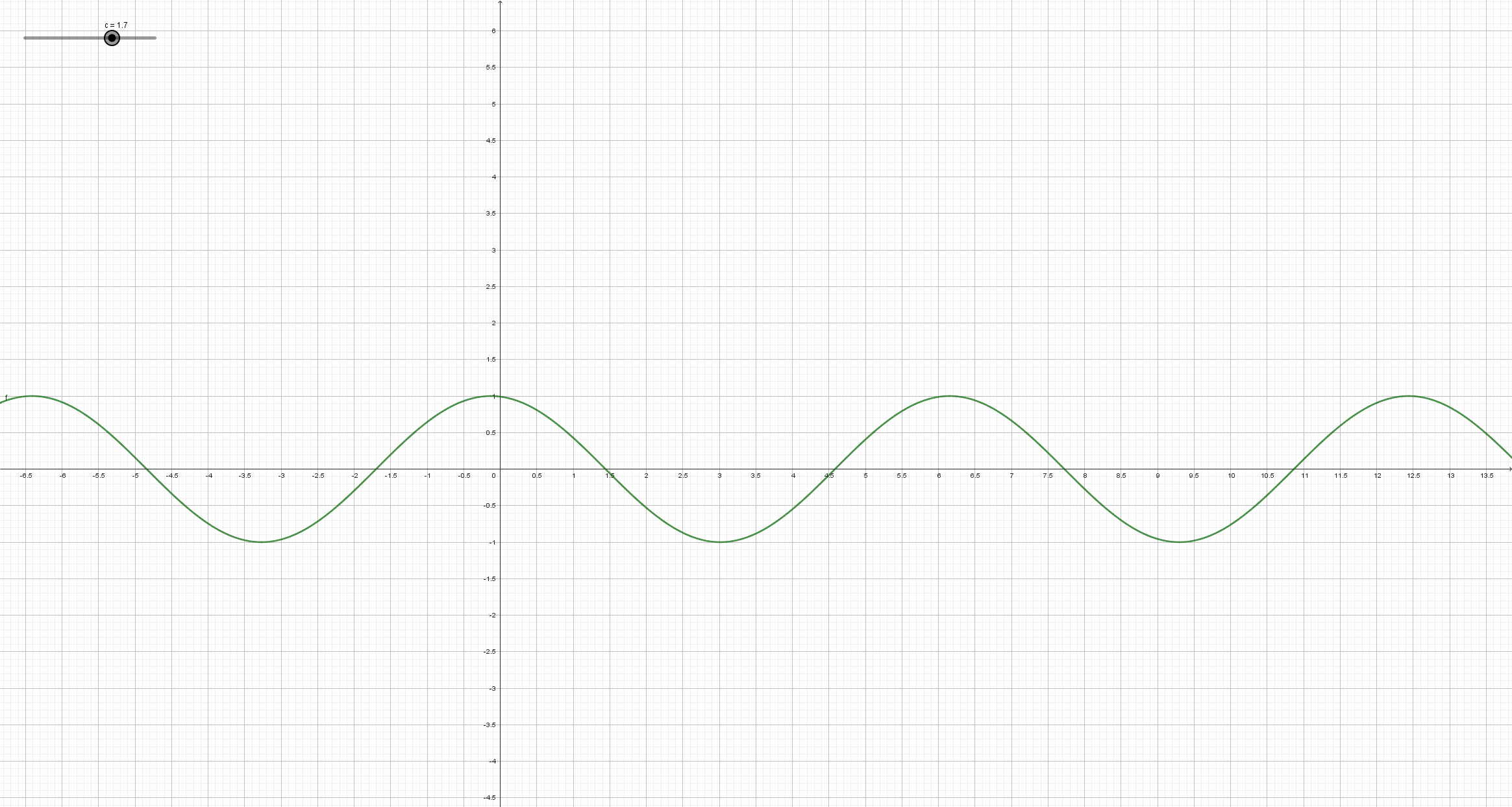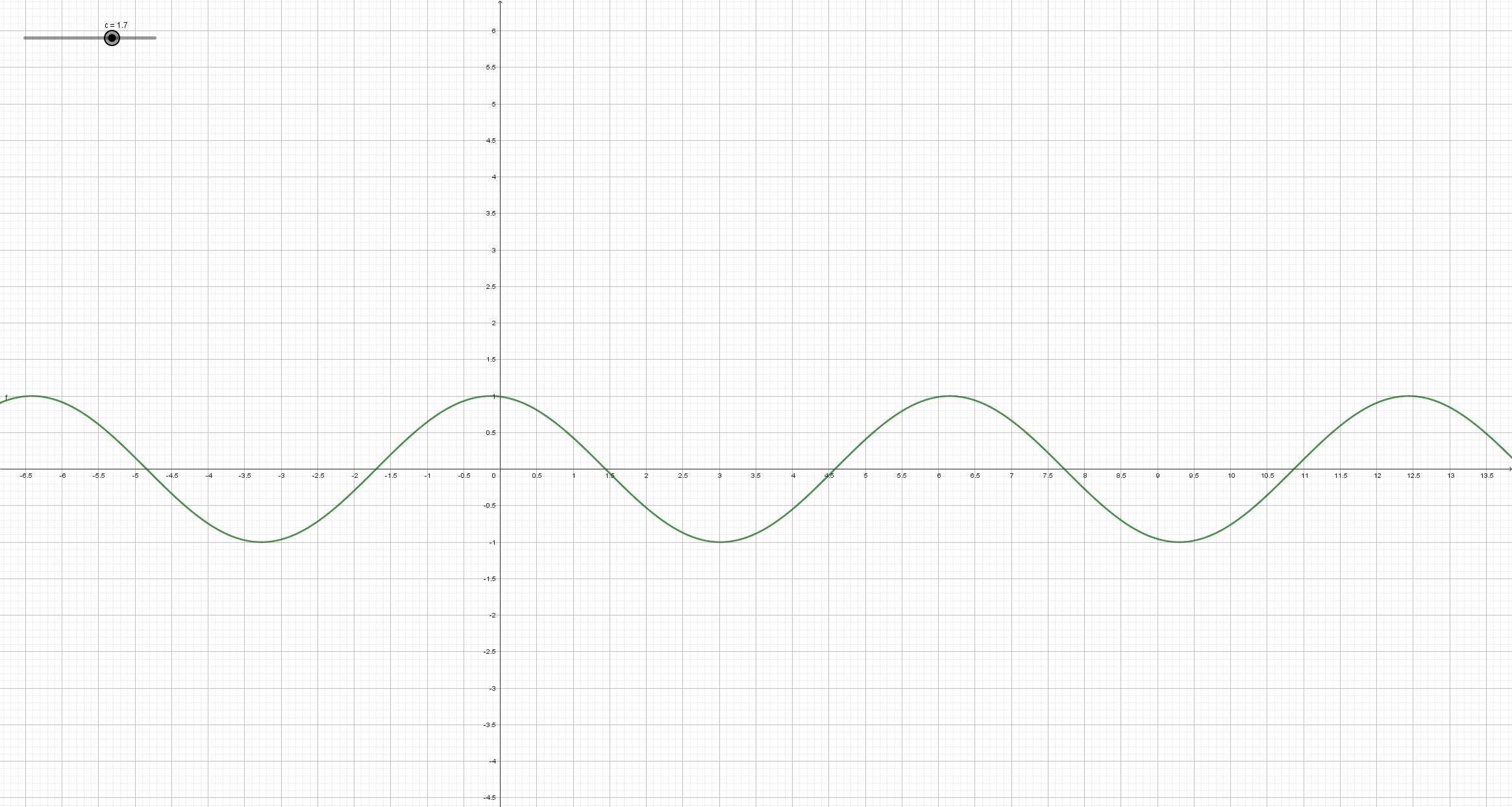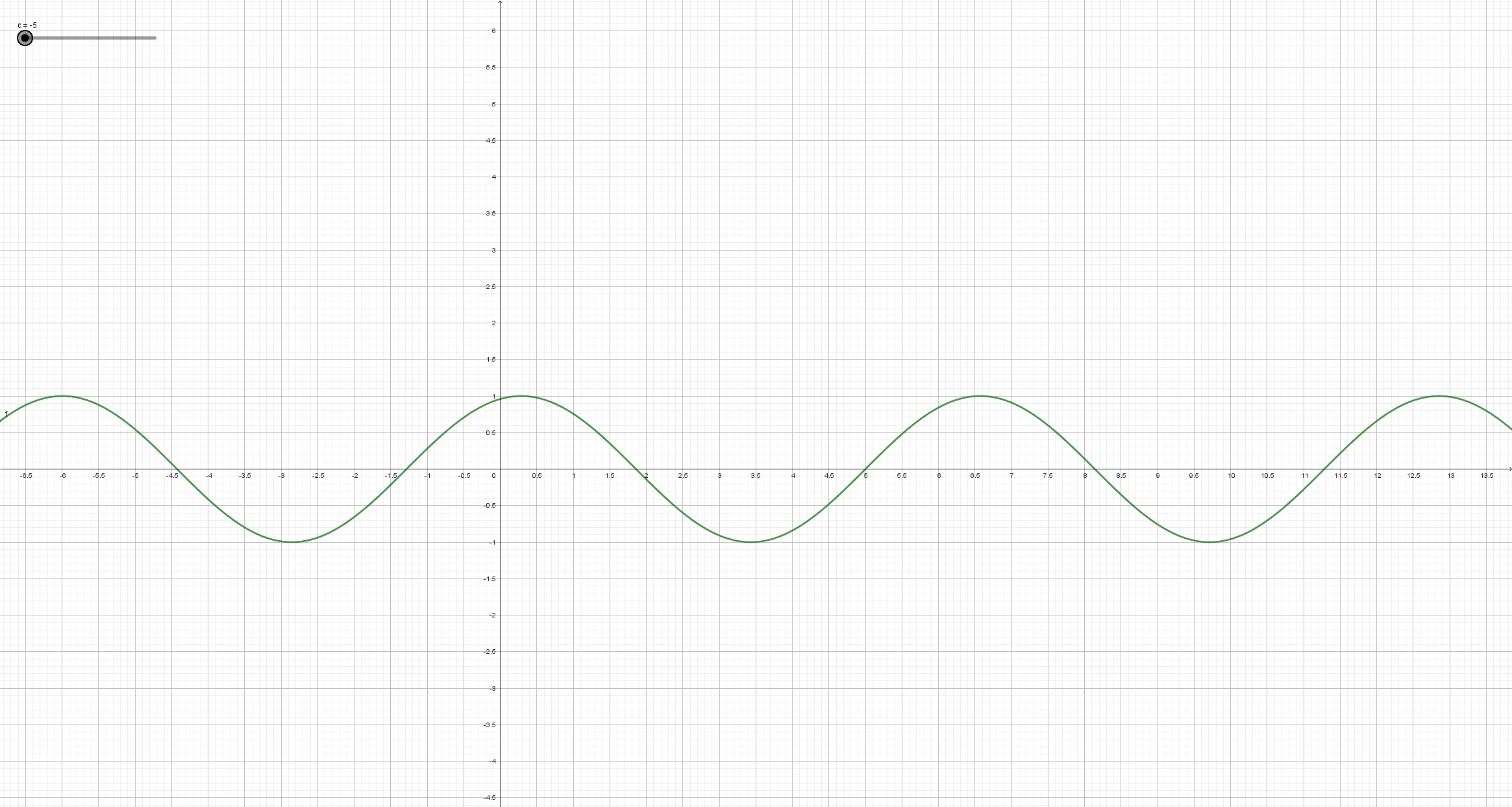
Beobachte, wie sich der Graph der Sinusfunktion y = a*sin(b*x+c)+d (mit a=1, b=1, d=0) ändert, wenn sich der Parameter c ändert. Schreibe deine Beobachtungsergebnisse so ausführlich wie möglich auf, und vergleiche mit der Lösung in dem entsprechendem Abschnitt auf dem Reiter "Lösungen".

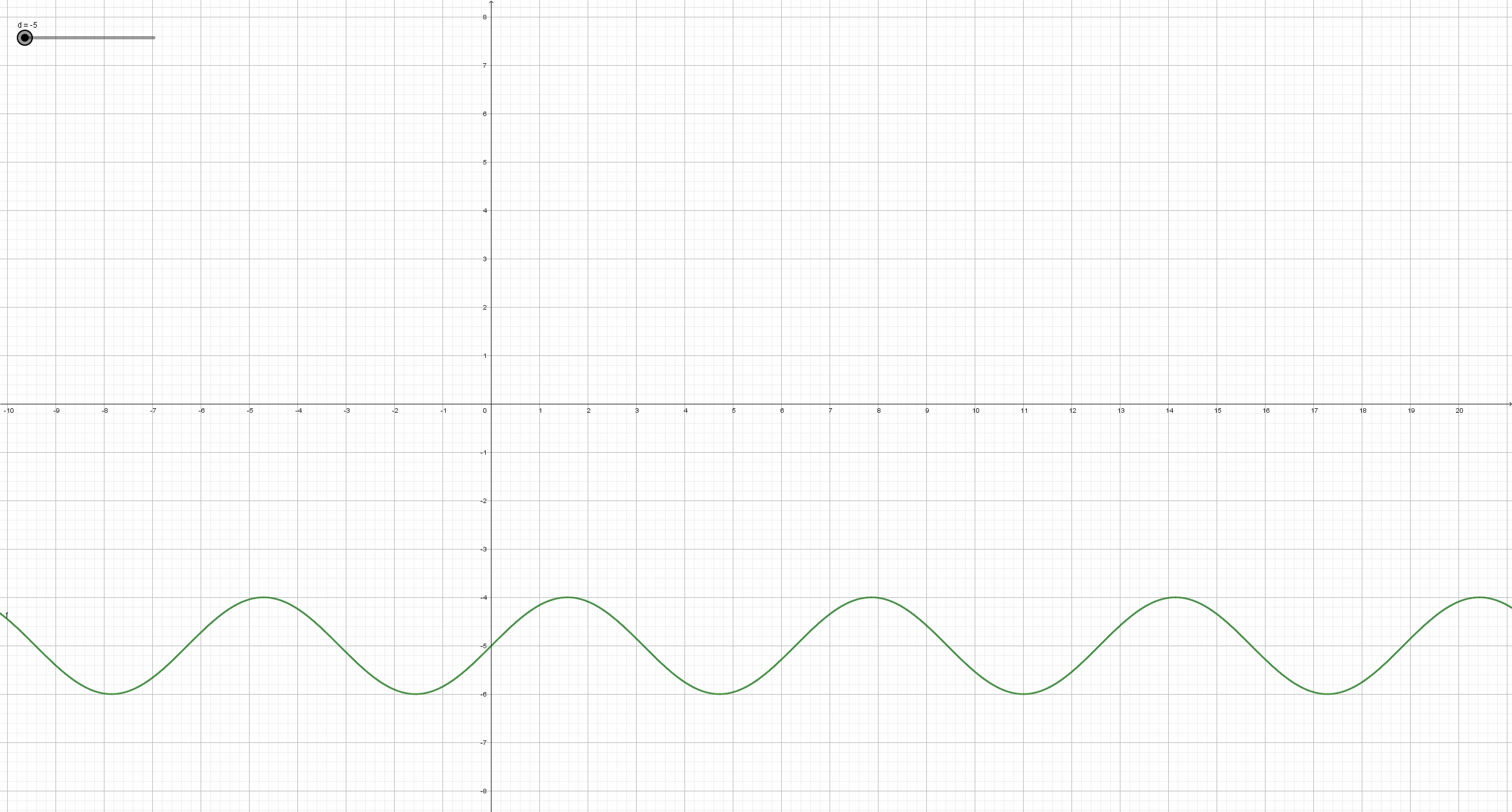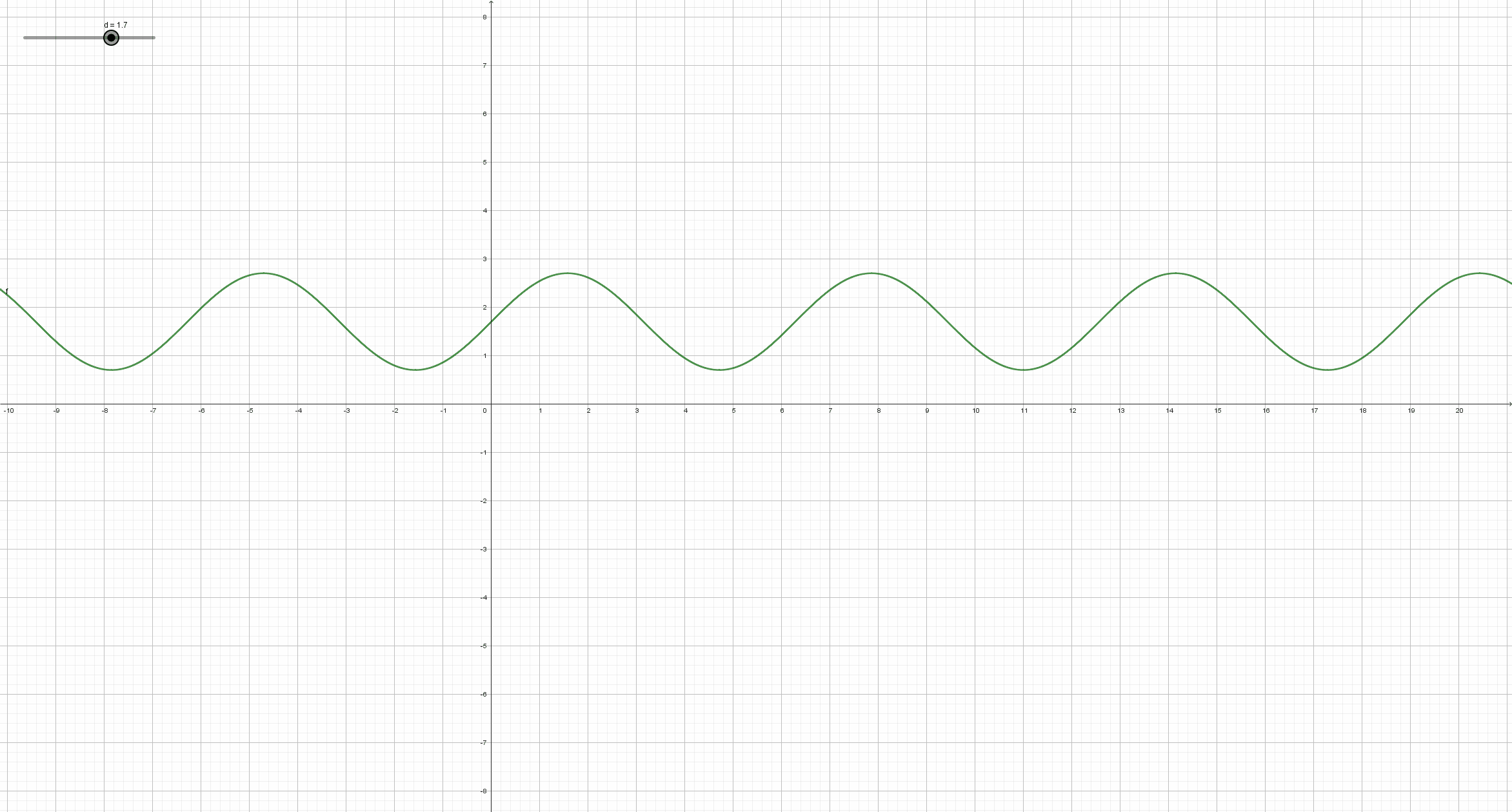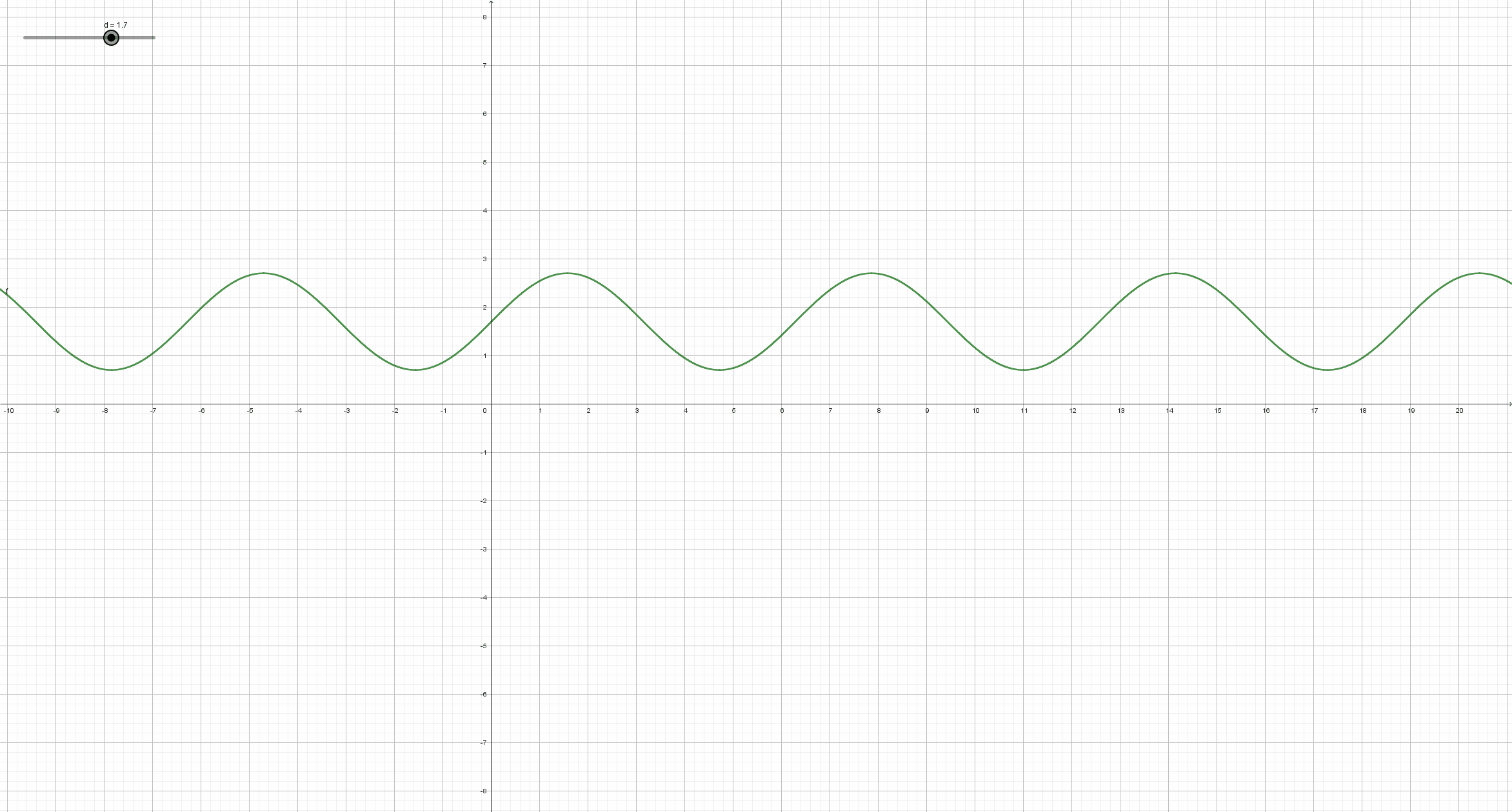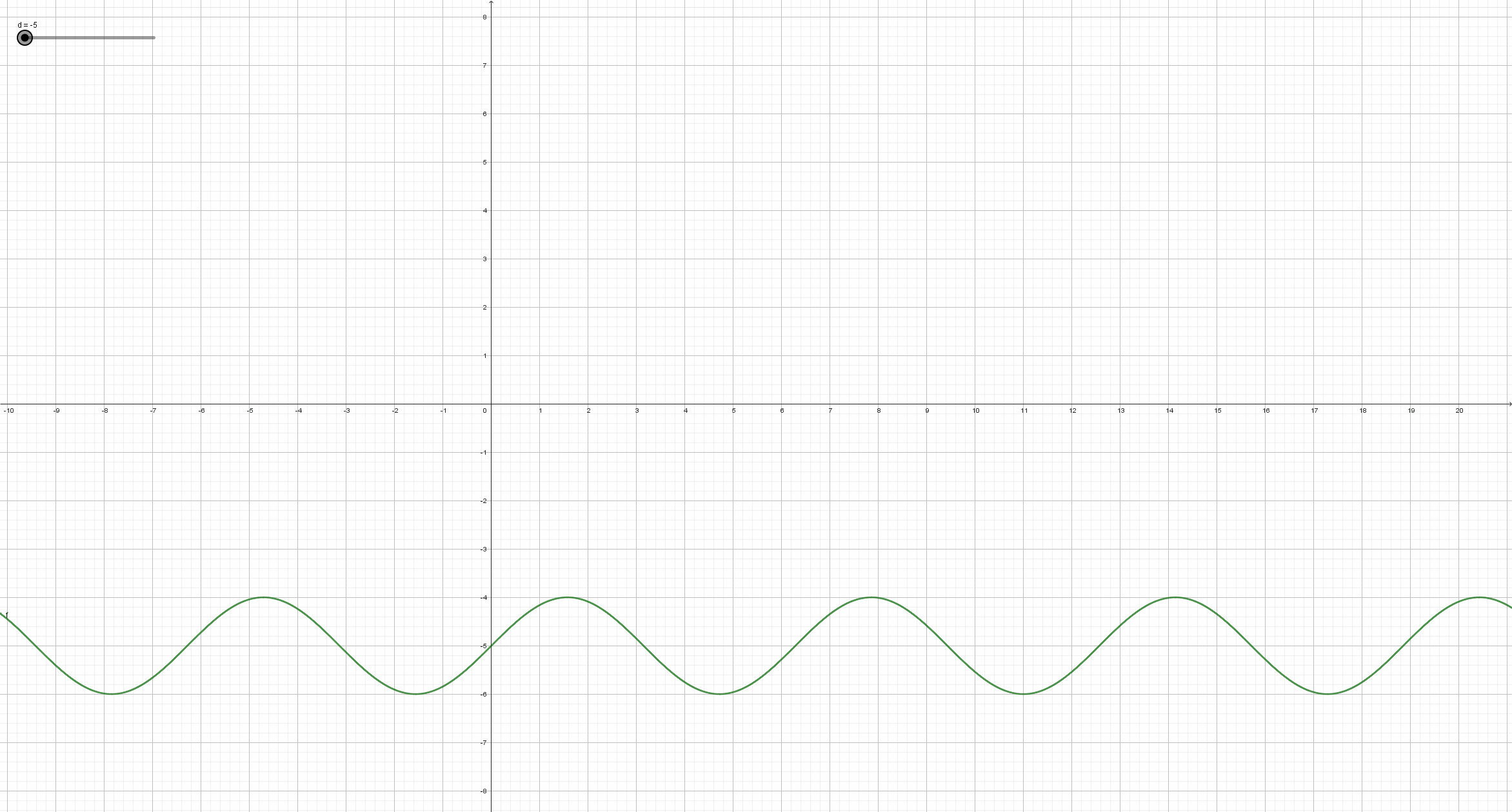
Beobachte, wie sich der Graph der Sinusfunktion y = a*sin(b*x+c)+d (mit a=1, b=1, c=0) ändert, wenn sich der Parameter d ändert. Schreibe deine Beobachtungsergebnisse so ausführlich wie möglich auf, und vergleiche mit der Lösung im entsprechendem Abschnitt auf dem Reiter "Lösungen".

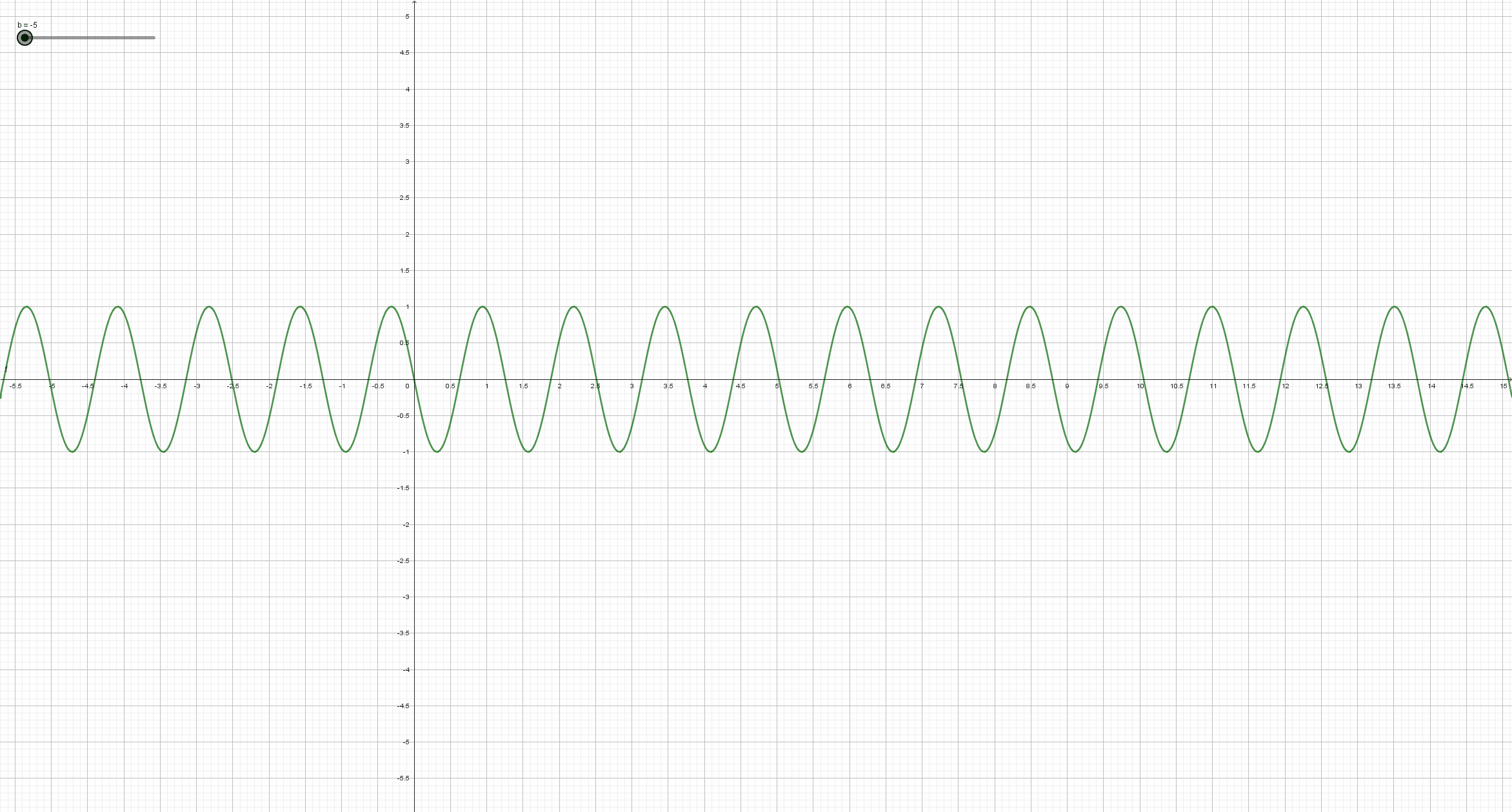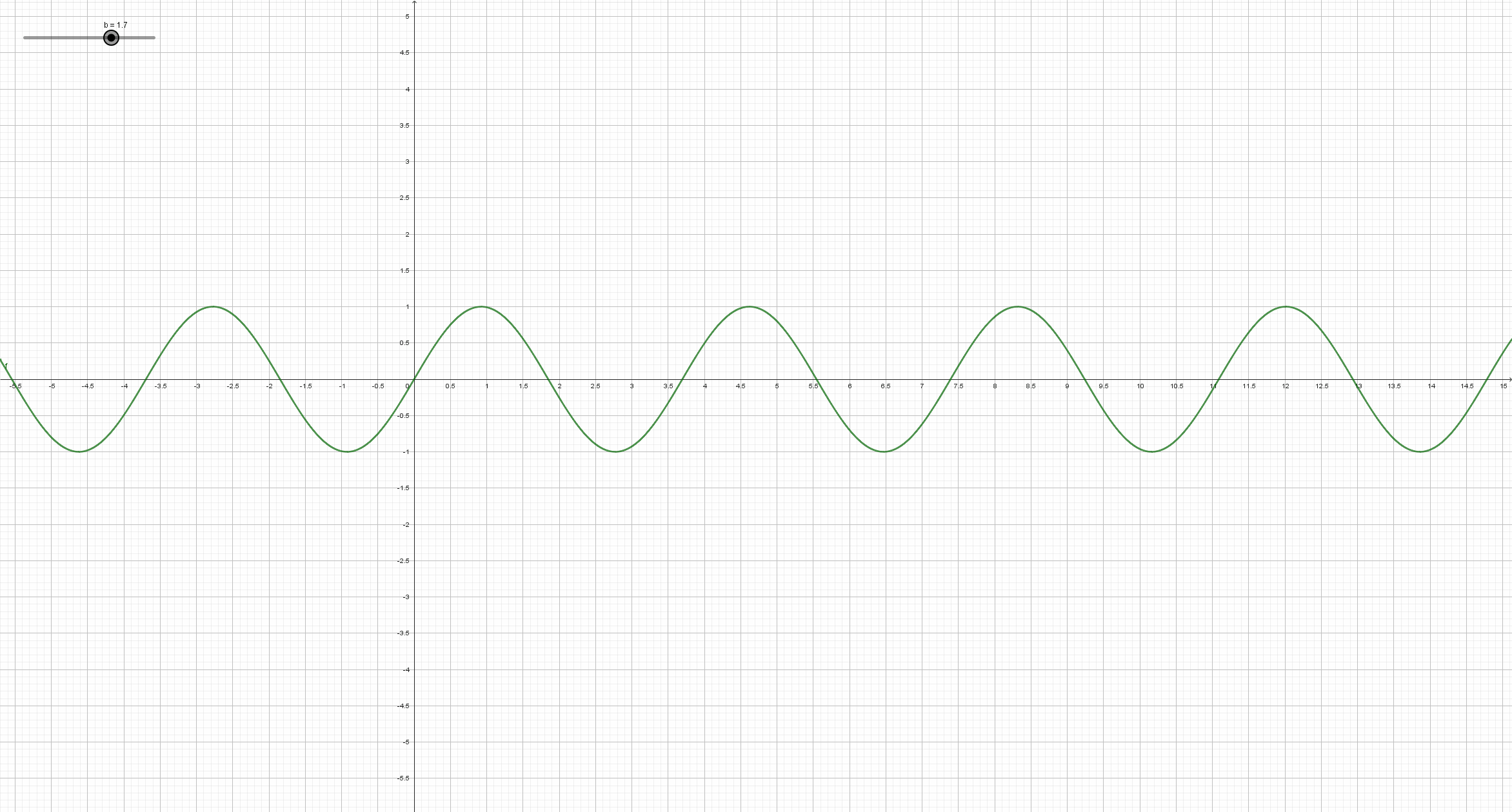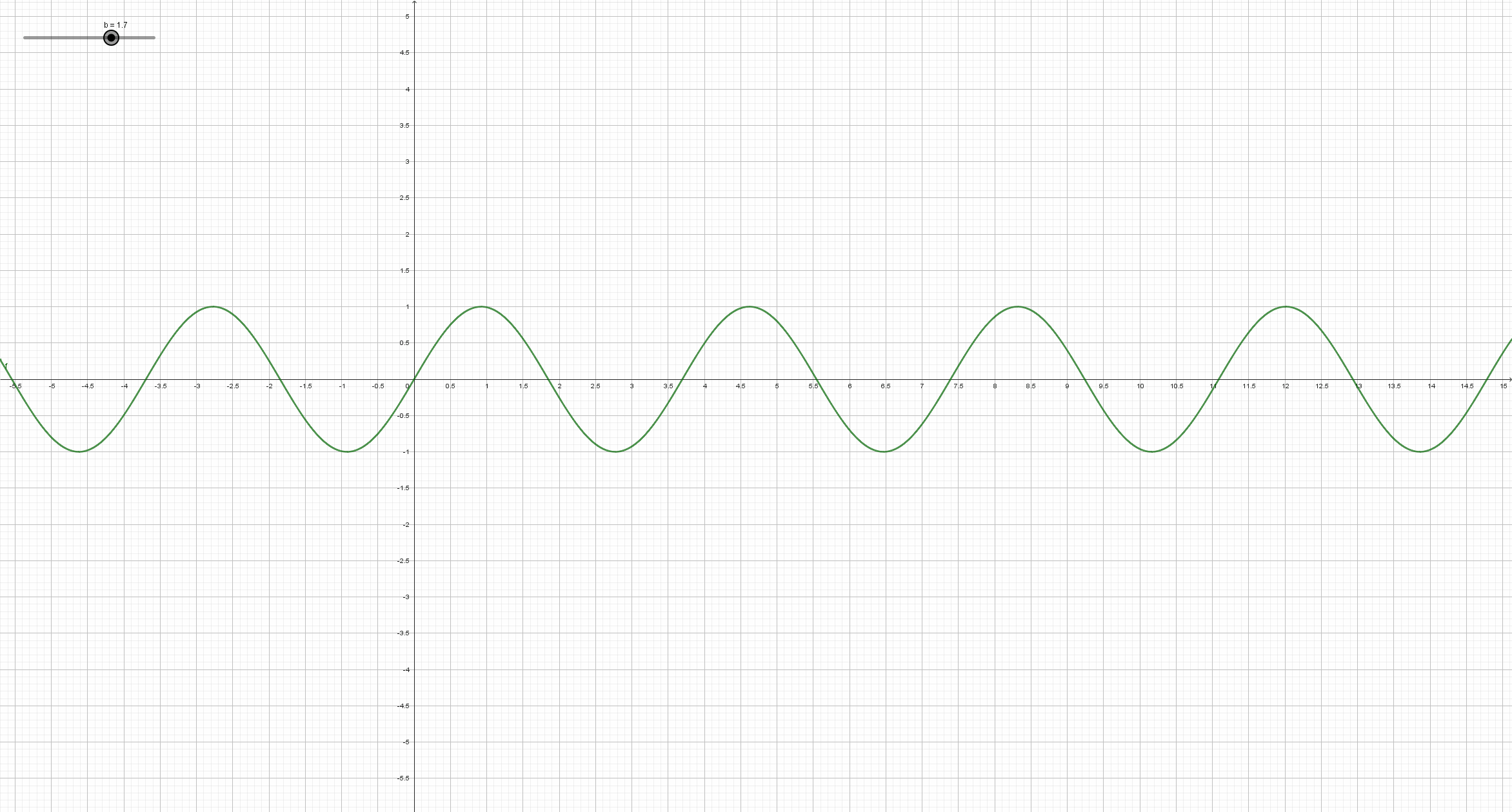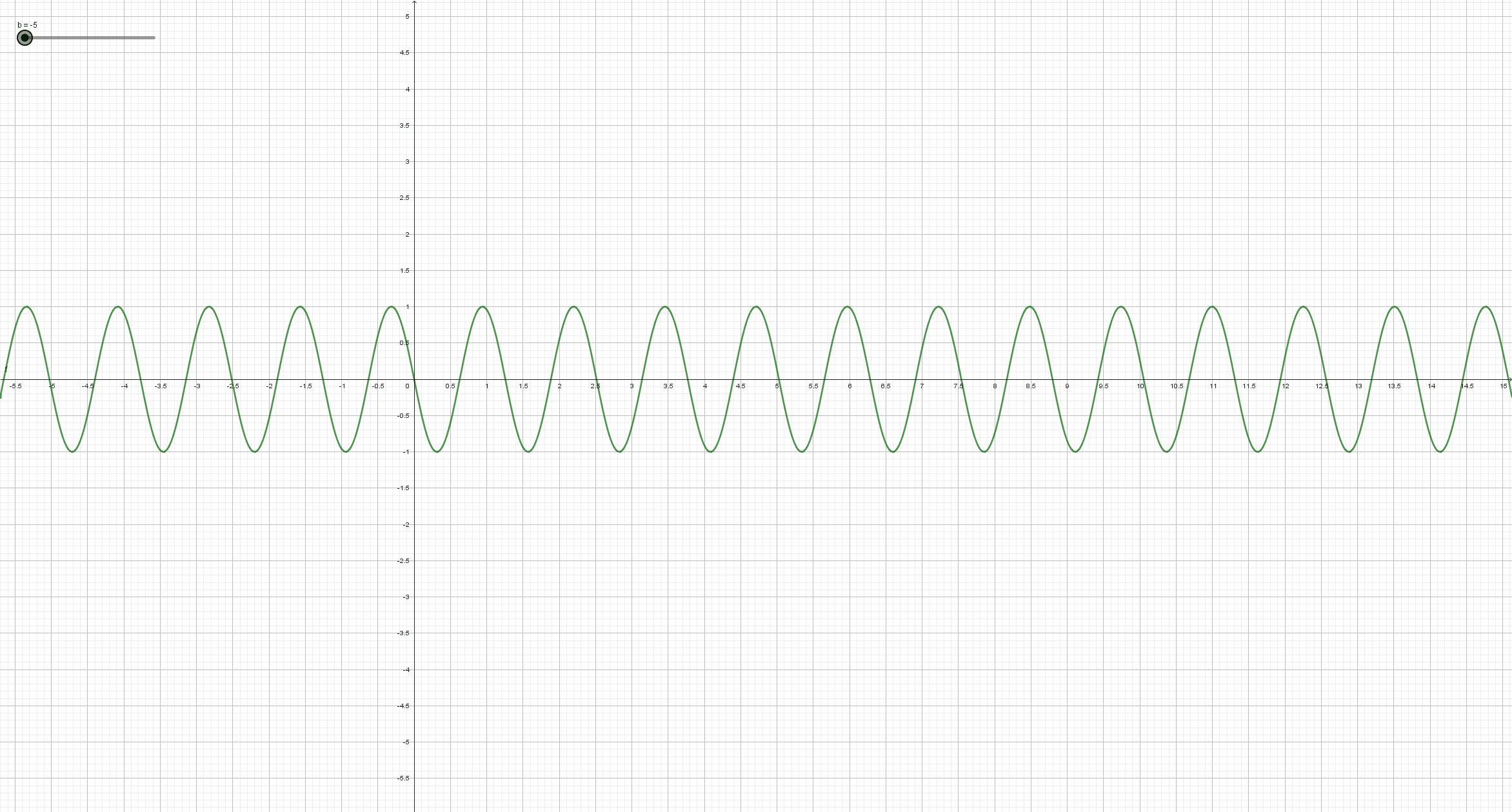
Beobachte, wie sich der Graph der Sinusfunktion y = a*sin(b*x+c)+d (mit a=1, c=0, d=0) ändert, wenn sich der Parameter b ändert. Schreibe deine Beobachtungsergebnisse so ausführlich wie möglich auf, und vergleiche mit der Lösung in dem entsprechendem Abschnitt auf dem Reiter "Lösungen".

Parameter a

Man erhält den Graph der Funktion y = a sin(x) aus dem Graph der Sinusfunktion durch Streckung oder Stauchung in Richtung der y-Achse. Genauer:  Ist der Betrag von a größer als eins, so wird der Graph der Sinusfunktion in y-Richtung mit dem Faktor Betrag von a gestreckt.  Ist der Betrag von a kleiner als eins, so wird der Graph der Sinusfunktion in y-Richtung mit dem Faktor Betrag von a gestaucht. Falls a negativ ist, so wird der Graph zusätzlich an der x-Achse gespiegelt.

Der Betrag von a wird auch als Amplitude bezeichnet.

Parameter c

Man erhält den Graph der Funktion y = sin( x + c ) aus dem Graph der Sinusfunktion durch Verschiebung in Richtung der x-Achse. Genauer: Ist c positiv, so wird der Graph der Sinusfunktion um den Betrag von c nach links verschoben. Ist c negativ, so wird der Graph der Sinusfunktion um den Betrag von c nach rechts verschoben.

c wird auch als Phasenverschiebung bezeichnet.

Parameter d

Man erhält den Graph der Funktion y = sin(x) + d aus dem Graph der Sinusfunktion durch Verschiebung in Richtung der y-Achse. Genauer: Ist d positiv, so wird der Graph der Sinusfunktion um den Betrag von d nach oben verschoben. Ist d negativ, so wird der Graph der Sinusfunktion um den Betrag von d nach unten verschoben.

Parameter b

Man erhält den Graph der Funktion y = sin(bx) aus dem Graph der Sinusfunktion durch Streckung oder Stauchung in Richtung der x-Achse. Genauer: Ist der Betrag von b größer als eins, so wird der Graph der Sinusfunktion in x-Richtung mit dem Faktor Betrag von 1/b gestaucht. Ist der Betrag von b kleiner als eins, so wird der Graph der Sinusfunktion in x-Richtung mit dem Faktor Betrag von 1/b gestreckt. Falls b negativ ist, so wird der Graph zusätzlich an der y-Achse gespiegelt.

Die Periode der Funktion ist 2 π/b. D.h.wenn man z.B. b verdoppelt, so halbiert sich die Periode.

1.) Zeichne die Graphen in ein- und dasselbe Koordinatensystem mit verschiedenen Farben und vergleiche! Kontrolliere deine Graphen mit GeoGebra!

a) y=sin(x)

b) y= 3*sin(x)

c) y=sin(πx)

d) y=sin(x)+3

2.) Zeichne den Graphen von y=2*sin(2x-1)+4 und beschreibe deine Vorgehensweise! Kontrolliere deinen Graphen mit GeoGebra!