Archimedes von Syrakus

Ungefähr 250 v. Chr. begann Archimedes, den Kreisumfang durch einbeschriebene und umbeschriebene regelmäßige Polygone zu approximieren. Wenn man die Anzahl der Polygonecken jeweils verdoppelt, so nähern sich die Polygonumfänge immer mehr dem Kreisumfang:

$\lim\limits_{n\to\infty}U_{n-Eck}=U_{Kreis}$

In den folgenden Rechnungen wird der Radius gleich 1 gesetzt, so dass $π=\frac{U}{2}$ gilt.

Die untere Skizze veranschaulicht, wie Archimdes beim einbeschriebenen Polygon vorgegangen ist: M ist der Mittelpunkt des Kreises und der Radius ist r=1.  Die Seite eines regelmäßigen Sechsecks ist $\overline{AC}=s_{n}$. Bei der Verdopplung zum Zwölfeck entstehen die Seiten $\overline{AB}$ und $\overline{BC}$ und werden mit $s_{2n}$ bezeichnet. In der nun folgenden Rechnung wird die Beziehung zwischen $s_{n}$ und $s_{2n}$ ermittelt.

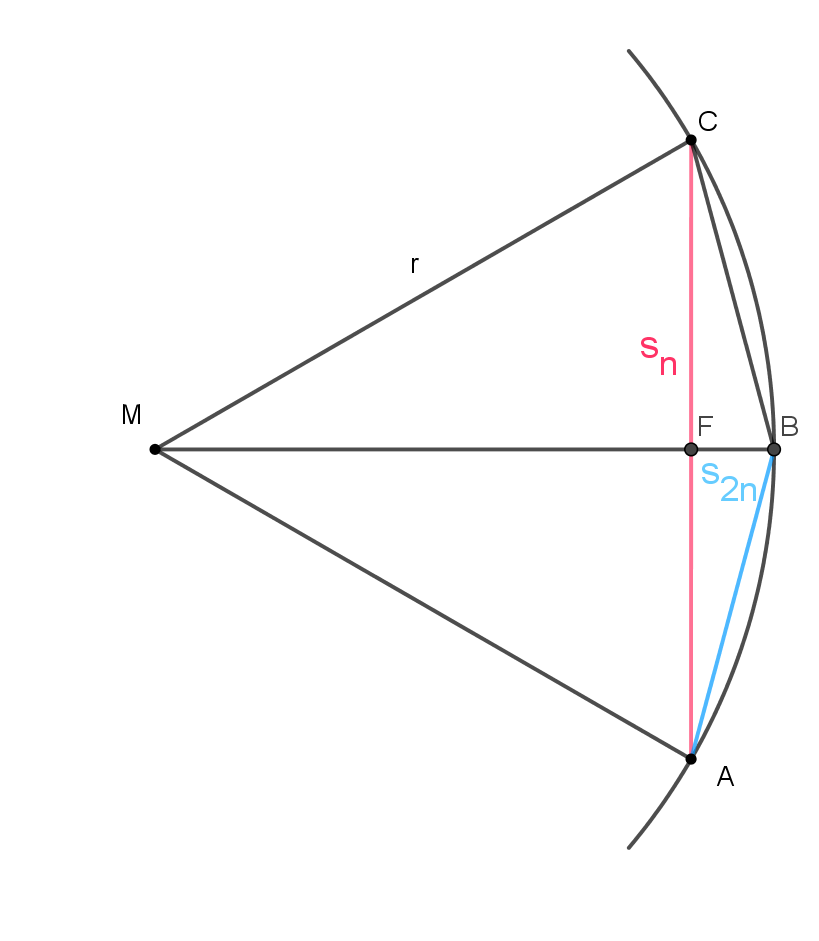
Da $\overline{MA}=r=1$ ist, folgt aus dem Satz des Pythagoras:

$\overline{AF}^{2}+\overline{MF}^{2} = 1 ⇔ \overline{MF}^{2} = 1 - \overline{AF}^{2}$

Für $\overline{AF} = \frac{s_{n}}{2}$ erhält man:

$\overline{MF} = \sqrt{1-(\frac{s_{n}}{2})^{2}}$ ⇔ $\overline{MF} = \frac{1}{2}\sqrt{4-s_{n}^{2}}  (1)$

Aus dem Satz des Pythagoras folgt auch: $\overline{AF}^{2} + \overline{FB}^{2} = \overline{AB}^{2} ⇔ \overline{FB}^{2} = \overline{AB}^{2} - \overline{AF}^{2}$

Mit $\overline{AB} = s_{2n}$ erhält man: $\overline{FB}=\sqrt{s_{2n}^{2}-(\frac{s_{n}}{2})^{2}} ⇔ \overline{FB} = \frac{1}{2}\sqrt{4s_{2n}^{2} - s_{n}^{2}}  (2)$

Es gilt $\overline{MF} + \overline{FB} = 1$ und mit den Formeln (1) und (2) folgt:

$\frac{1}{2}\sqrt{4 - s_{n}^{2}} + \frac{1}{2}\sqrt{4s_{2n}^{2} - s_{n}^{2}} = 1 ⇔ 1 - \frac{1}{2}\sqrt{4 - s_{n}^{2}} = \frac{1}{2}\sqrt{4s_{2n}^{2} - s_{n}^{2}}$

Jetzt werden beide Seiten quadriert:

$1 - 2 ⋅\frac{1}{2}\sqrt{4 - s_{n}^{2}} + \frac{1}{4}(4-s_{n}^{2}) = \frac{1}{4}(4s_{2n}^{2} - s_{n}^{2})$

⇔ $1-\sqrt{4 - s_{n}^{2}} + 1 - \frac{s_{n}^{2}}{4} = s_{2n}^{2} - \frac{s_{n}^{2}}{4}$

⇔ $s_{2n}^{2} = 2 - \sqrt{4 - s_{n}^{2}} ⇔ \underline{s_{2n} = \sqrt{2 - \sqrt{4 - s_{n}^{2}}}}$

Für den Umfang multipliziert man das $s_{2n}$ mit 2n: $\underline{u_{2n} = 2n ⋅ s_{2n}}$

Im nächsten Reiter führen wir ähnliche Rechnungen für die Approximation durch umbeschriebene Polygone durch.